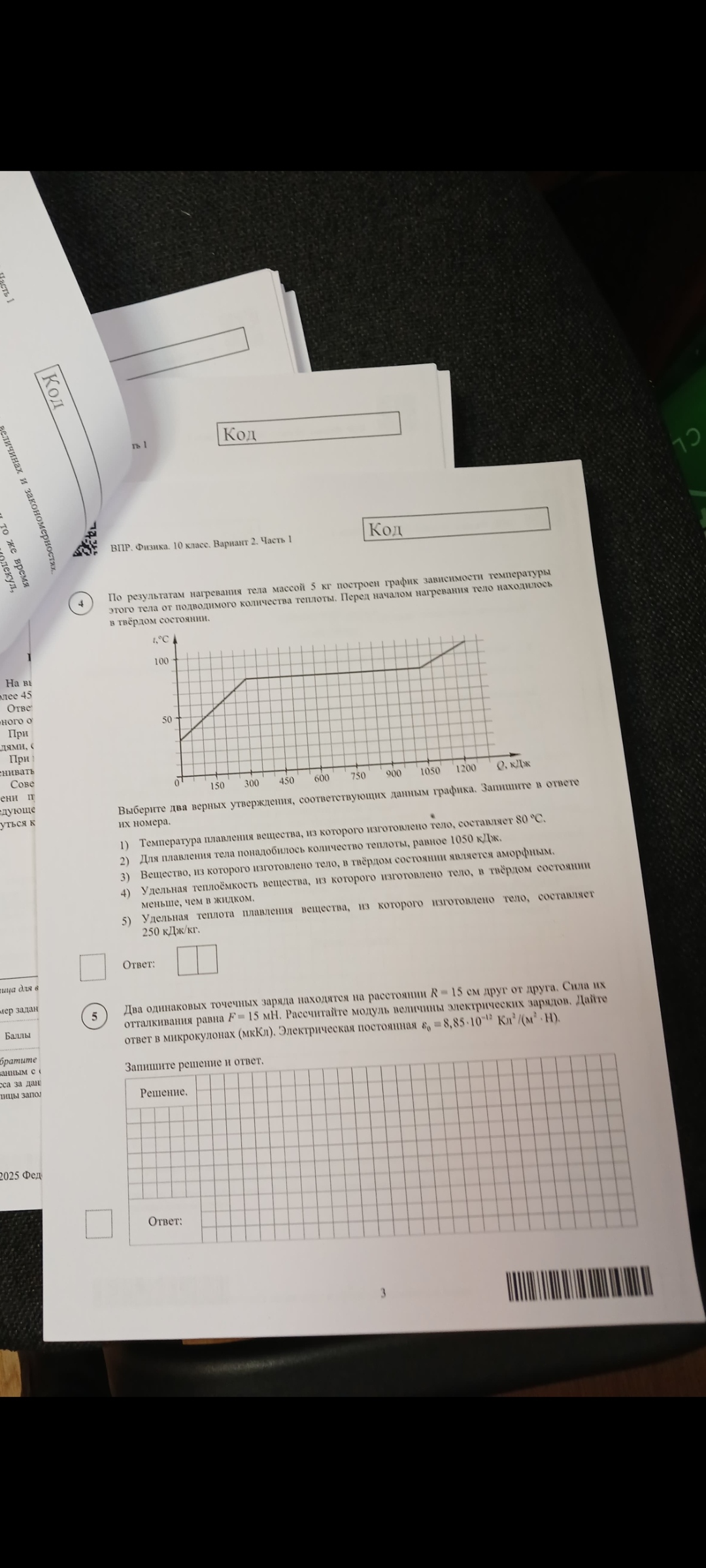
Задание 5: Два одинаковых точечных заряда находятся на расстоянии \(R = 15 \text{ см} \) друг от друга. Сила их отталкивания равна \(F = 15 \text{ мН} \). Рассчитайте модуль величины электрических зарядов. Дайте ответ в микрокулонах (мкКл). Электрическая постоянная \( \varepsilon_0 = 8,85 \cdot 10^{-12} \frac{\text{Кл}^2}{\text{м}^2 \cdot \text{Н}} \).

Закон Кулона описывает силу взаимодействия между двумя точечными зарядами: \[ F = k \frac{|q_1 q_2|}{R^2} \] где \( F \) - сила взаимодействия, \( q_1 \) и \( q_2 \) - величины зарядов, \( R \) - расстояние между зарядами, и \( k \) - коэффициент Кулона, который можно выразить через электрическую постоянную \( \varepsilon_0 \): \[ k = \frac{1}{4 \pi \varepsilon_0} \] В нашем случае, заряды одинаковы (\( q_1 = q_2 = q \)), поэтому формулу можно переписать так: \[ F = k \frac{q^2}{R^2} \] Или: \[ F = \frac{1}{4 \pi \varepsilon_0} \frac{q^2}{R^2} \] Нам нужно найти \( q \), поэтому выразим его из формулы: \[ q^2 = 4 \pi \varepsilon_0 F R^2 \] \[ q = \sqrt{4 \pi \varepsilon_0 F R^2} \] Подставим известные значения: \( R = 15 \text{ см} = 0,15 \text{ м} \), \( F = 15 \text{ мН} = 0,015 \text{ Н} \), \( \varepsilon_0 = 8,85 \cdot 10^{-12} \frac{\text{Кл}^2}{\text{м}^2 \cdot \text{Н}} \) \[ q = \sqrt{4 \pi \cdot 8,85 \cdot 10^{-12} \cdot 0,015 \cdot (0,15)^2} \] \[ q = \sqrt{4 \pi \cdot 8,85 \cdot 10^{-12} \cdot 0,015 \cdot 0,0225} \] \[ q \approx \sqrt{3,745 \cdot 10^{-14}} \] \[ q \approx 1,935 \cdot 10^{-7} \text{ Кл} \] Теперь переведем в микрокулоны: \[ q \approx 1,935 \cdot 10^{-7} \text{ Кл} = 0,1935 \cdot 10^{-6} \text{ Кл} = 0,1935 \text{ мкКл} \] Округлим до сотых: \[ q \approx 0,19 \text{ мкКл} \] Ответ: 0,19 мкКл