Установите соответствие между графиками функций и формулами, которые они задают 1) y=корень из x; 2) y=2/x;

Ответ:

3) y=x/2

4) y=x^3

\[- 24; - 12; - 6;\ldots\]

\[b_{1} = - 24;\ \ b_{2} = - 12:\]

\[q = \frac{b_{2}}{b_{1}} = \frac{- 12}{- 24} = \frac{1}{2}.\]

\[S_{5} = \frac{b_{1} \cdot \left( 1 - q^{5} \right)}{1 - q} = \frac{- 24 \cdot \left( 1 - \left( \frac{1}{2} \right)^{5} \right)}{1 - \frac{1}{2}} =\]

\[= \frac{- 24 \cdot \left( 1 - \frac{1}{32} \right)}{\frac{1}{2}} = - 48 \cdot \frac{31}{32} =\]

\[= \frac{- 3 \cdot 31}{2} = - \frac{93}{2} = - 46,5.\]

\[Ответ:\ - 46,5.\]

\[\frac{4x^{2}}{2x - 1} + \frac{1}{1 - 2x} - 2x - 7 =\]

\[= \frac{4x^{2}}{2x - 1} - \frac{1}{2x - 1} - (2x + 7)^{\backslash 2x - 1} =\]

\[= \frac{4x^{2} - 1 - 4x^{2} - 14x + 2x + 7}{2x - 1} =\]

\[= \frac{- 12x + 6}{2x - 1} = \frac{- 6(2x - 1)}{2x - 1} = - 6.\]

\[Ответ:\ - 6.\]

\[\frac{3 - 2x}{x + 2} + 1^{\backslash x + 2} \leq 0\]

\[\frac{3 - 2x + x + 2}{x + 2} \leq 0\]

\[\frac{- x + 5}{x + 2} \leq 0;\ \ \ \ \ x \neq - 2\]

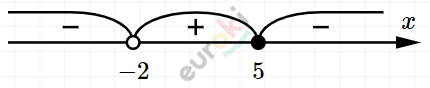
\[x < - 2;\ \ x \geq 5.\]

\[Ответ:4.\]

\[Ответ:3.\]

\[Ответ:третьего\ числа.\]

\[10\ 080\ рублей - 112\%\]

\[x\ рублей - 100\%\]

\[x = \frac{10\ 080 \cdot 100}{112} = 90 \cdot 100 =\]

\[= 9000\ (рублей) - стоит\ стиральная\]

\[машина.\]

\[Ответ:9000\ рублей.\]