Упростите выражение и найдите его значение: (x-4y)^2-(4x-y)^2, если x = 1 1/3, y = -2.

\[(x - 4y)^{2} - (4x - y)^{2} =\]

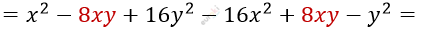
\[= - 15x^{2} + 15y^{2} =\]

\[= - 15 \cdot \left( x^{2} - y^{2} \right)\]

\[при\ \ x = 1\frac{1}{3} = \frac{4}{3};\ \ y = - 2:\]

\[- 15 \cdot \left( \frac{16}{9} - 4 \right) =\]

\[= - 15 \cdot \left( - \frac{20}{9} \right) = \frac{100}{3} = 33\frac{1}{3}.\]