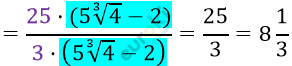Упростите выражение: 41/(5-корень 3 степени из 2)-(10+2*корень 3 степени из 2)/(3*корень 3 степени из 4).

\[\frac{41^{\backslash 3\sqrt[3]{4}}}{5 - \sqrt[3]{2}} - \frac{10 + 2{\sqrt[3]{2}}^{\backslash 5 - \sqrt[3]{2}}}{3\sqrt[3]{4}} =\]

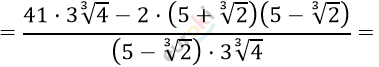
\[= \frac{123\sqrt[3]{4} - 2 \cdot \left( 5^{2} - \left( \sqrt[3]{2} \right)^{2} \right)}{\left( 5 - \sqrt[3]{2} \right) \cdot 3\sqrt[3]{4}} =\]

\[= \frac{123\sqrt[3]{4} - 2 \cdot \left( 25 - \sqrt[3]{4} \right)}{3 \cdot \left( 5\sqrt[3]{4} - \sqrt[3]{8} \right)} =\]

\[= \frac{125\sqrt[3]{4} - 50}{3 \cdot \left( 5\sqrt[3]{4} - \sqrt[3]{8} \right)} =\]