Турист, проплыл по течению реки на плоту 12 км, возвратился обратно на лодке, скорость которой в стоячей воде 6 км/ч. Найдите скорость течения реки, если известно, что на все путешествие турист затратил 8 ч.

\[x\frac{км}{ч - скорость\ течения;}\]

\[\frac{12}{x}\ ч - по\ течению;\]

\[\frac{12}{6 - x}\ ч - против\ течения.\]

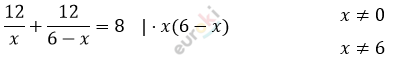
\[12 \cdot (6 - x) + 12x = 8x(6 - x)\]

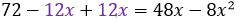
\[8x^{2} - 48x + 72 = 0\ \ \ \ \ \ |\ :8\]

\[x^{2} - 6x + 9 = 0\]

\[(x - 3)^{2} = 0\]

\[(x - 3) = 0\]

\[x = 3\]

\[Ответ:3\frac{км}{ч.}\]