Решите уравнение: (y+3)/(9y^2+3y+1)+3/(27y^3-1)=1/(3y-1).

Ответ:

\[\frac{y + 3}{9y^{2} + 3y + 1} + \frac{3}{27y^{3} - 1} =\]

\[= \frac{1}{3y - 1}\text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }\]

\[ОДЗ:\ \ y \neq \frac{1}{3}\]

\[\frac{3}{(3y - 1)\left( 9y^{2} + 3y + 1 \right)} =\]

\[= \frac{1}{3y - 1} - \frac{y + 3}{9y² + 3y + 1}\]

\[\frac{3}{(3y - 1)\left( 9y^{2} + 3y + 1 \right)} =\]

\[= \frac{9y^{2} + 3y + 1 - (y + 3)(3y - 1)}{(3y - 1)\left( 9y^{2} + 3y + 1 \right)}\]

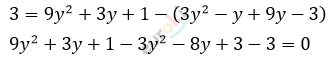
\[6y^{2} - 5y + 1 = 0\]

\[D = b^{2} - 4ac = 25 - 4 \cdot 6 \cdot 1 =\]

\[= 25 - 24 = 1\]

\[y_{1} = \frac{5 + 1}{12} = \frac{6}{12} = \frac{1}{2}\]

\[y_{2} = \frac{5 - 1}{12} = \frac{4}{12} =\]

\[= \frac{1}{3}\ \ (не\ подходит\ по\ ОДЗ)\]

\[Ответ:y = \frac{1}{2}.\]