Решите уравнение: x^3+3x^2-3x+4=0.

\[x³ + 3x² - 3x + 4 = 0\]

\[P(1) = 1^{3} + 3 \bullet 1^{2} - 3 \bullet 1 + 4 =\]

\[= 1 + 3 - 3 + 4 = 5
eq 0\]

\[P( - 1) =\]

\[= ( - 1)^{3} + 3 \bullet ( - 1)^{2} - 3 \bullet ( - 1) + 4 =\]

\[= - 1 + 3 + 3 + 4 = 9
eq 0\]

\[P(2) = 2^{3} + 3 \bullet 2^{2} - 3 \bullet 2 + 4 =\]

\[= 8 + 12 - 6 + 4 = 18
eq 0\]

\[P( - 2) =\]

\[= ( - 2)^{3} + 3 \bullet ( - 2)^{2} - 3 \bullet 4 + 4 =\]

\[= - 8 + 6 + 6 + 4 = 8
eq 0\]

\[P(4) = 4^{3} + 3 \bullet 4^{2} - 3 \bullet 4 + 4 =\]

\[= 64 + 48 - 12 + 4 = 104
eq 0\]

\[P( - 4) =\]

\[= ( - 4)^{3} + 3 \bullet ( - 4)^{2} - 3 \bullet ( - 4) + 4 =\]

\[= - 64 + 48 + 12 + 4 = 0\]

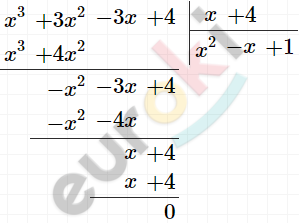
\[(x + 4)(x² - x + 1) = 0\]

\[x + 4 = 0\]

\[x = - 4.\]

\[x^{2} - x + 1 = 0\]

\[D = ( - 1)^{2} - 4 \bullet 1 \bullet 1 = 1 - 4 =\]

\[= - 3 < 0 \Longrightarrow нет\ решений.\]

\[Ответ:\ - 4.\]