Решите систему уравнений: y+x=7; 4/x+3/y=2.

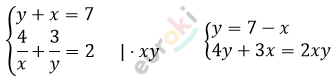
\[4 \bullet (7 - x) + 3x = 2x(7 - x)\]

\[28 - 4x + 3x = 14x - 2x^{2}\]

\[28 - x - 14x + 2x^{2} = 0\]

\[2x^{2} - 15x + 28 = 0\]

\[D = ( - 15)^{2} - 4 \cdot 2 \cdot 28 =\]

\[= 225 - 224 = 1\]

\[x_{1} = \frac{15 + \sqrt{1}}{2 \cdot 2} = \frac{15 + 1}{4} = \frac{16}{4} = 4\]

\[x_{2} = \frac{15 - \sqrt{1}}{2 \cdot 2} = \frac{15 - 1}{4} = \frac{14}{4} =\]

\[= 3\frac{2}{4} = 3,5\]

\[x_{1} = 4 \Longrightarrow \text{\ \ \ \ \ \ \ \ }y_{1} = 7 - 4 = 3.\]

\[x_{2} = 3,5 \Longrightarrow \text{\ \ \ \ }y_{2} = 7 - 3,5 =\]

\[= 3,5.\]

\[Ответ:(4;3),\ \ \ (3,5;3,5)\]