Решите систему уравнений: x^2-y^2=9; xy=20.

Ответ:

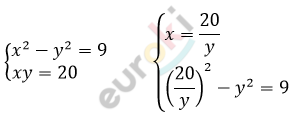
\[\frac{400}{y^{2}} - y^{2} = 9\ \ \ \ \ \ \ | \cdot y^{2};\ \ y \neq 0\]

\[400 - y^{4} - 9y^{2} = 0\]

\[y^{4} + 9y^{2} - 400 = 0\]

\[Пусть\ y^{2} = t \geq 0:\]

\[t^{2} + 9t - 400 = 0\]

\[D = 81 + 1600 = 1681 = 41^{2}\]

\[t_{1} = \frac{- 9 + 41}{2} = \frac{32}{2} = 16;\]

\[t_{2} = \frac{- 9 - 41}{2} = - \frac{50}{2} =\]

\[= - 25\ (не\ подходит).\]

\[y^{2} = 16\]

\[y = \pm 4.\]

\[\left\{ \begin{matrix} y = 4 \\ x = 5 \\ \end{matrix} \right.\ \ \ \ \ или\ \ \ \left\{ \begin{matrix} y = - 4 \\ x = - 5 \\ \end{matrix} \right.\ \]

\[Ответ:(5;4);\ \ ( - 5; - 4).\]