Решите систему уравнений x^2-5y-24=0; y=x-2 и выполните проверку.

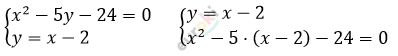
\[x^{2} - 5x + 10 - 24 = 0\]

\[x^{2} - 5x - 14 = 0\]

\[x_{1} + x_{2} = 5;\ \ \ x_{1} \cdot x_{2} = - 14\]

\[x_{1} = 7;\ \ \ x_{2} = - 2.\]

\[\left\{ \begin{matrix}
x = 7 \\
y = 5 \\
\end{matrix} \right.\ \ \ \ \ или\ \ \ \left\{ \begin{matrix}
x = - 2 \\
y = - 4 \\
\end{matrix} \right.\ \]

\[Проверка.\]

\[(7;5):\]

\[\left\{ \begin{matrix}
49 - 25 - 24 = 0 \\
5 = 7 - 2\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\
\end{matrix} \right.\ \text{\ \ \ \ \ \ \ }\left\{ \begin{matrix}
0 = 0 \\
5 = 5 \\
\end{matrix} \right.\ \rightarrow\]

\[\rightarrow верно.\]

\[( - 2; - 4):\]

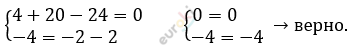
\[Ответ:(7;5);\ \ ( - 2; - 4).\]