Решите систему уравнений: x^2+y^2=5; xy=2.

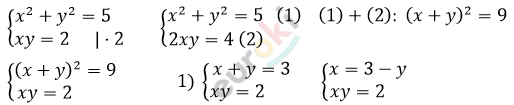
\[(3 - y)y = 2\]

\[3y - y^{2} = 2\]

\[y^{2} - 3y + 2 = 0\]

\[D = ( - 3)^{2} - 4 \cdot 1 \cdot 2 = 9 - 8 =\]

\[= 1\]

\[y_{1} = \frac{3 + \sqrt{1}}{2} = \frac{3 + 1}{2} = \frac{4}{2} = 2\]

\[y_{2} = \frac{3 - \sqrt{1}}{2} = \frac{3 - 1}{2} = \frac{2}{2} = 1\]

\[y_{1} = 2 \Longrightarrow \ \ \ \ \ \ \ x_{1} = 3 - 2 = 1.\]

\[y_{2} = 1 \Longrightarrow \ \ \ \ \ \ \ x_{2} = 3 - 1 = 2.\]

\[2)\ \left\{ \begin{matrix} x + y = - 3 \\ xy = 2\ \ \ \ \ \ \ \\ \end{matrix}\text{\ \ \ \ } \right.\ \left\{ \begin{matrix} x = - y - 3 \\ xy = 2\ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[( - y - 3)y = 2\]

\[- y^{2} - 3y = 2\]

\[y^{2} + 3y + 2 = 0\]

\[D = 3^{2} - 4 \cdot 1 \cdot 2 = 9 - 8 = 1\]

\[y_{3} = \frac{- 3 + \sqrt{1}}{2} = \frac{- 3 + 1}{2} = \frac{- 2}{2} =\]

\[= - 1\]

\[y_{4} = \frac{- 3 - \sqrt{1}}{2} = \frac{- 3 - 1}{2} = \frac{- 4}{2} =\]

\[= - 2\]

\[y_{3} = - 1 \Longrightarrow x_{3} = - ( - 1) - 3 =\]

\[= 1 - 3 = - 2.\]

\[y_{4} = - 2 \Longrightarrow x_{4} = - ( - 2) - 3 =\]

\[= 2 - 3 = - 1.\]

\[Ответ:(1;2),\ (2;1),\ ( - 2;\ - 1),\]

\[\ ( - 1;\ - 2).\]