Решите систему уравнений: 3/x+2/(y+2)=5; 4/x-3/(y+2)=1.

\[\left\{ \begin{matrix} \frac{3}{x} + \frac{2}{y + 2} = 5 \\ \frac{4}{x} - \frac{3}{y + 2} = 1\ \\ \end{matrix} \right.\ \]

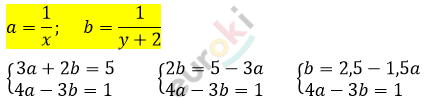
\[4a - 3 \bullet (2,5 - 1,5a) = 1\]

\[4a - 7,5 + 4,5a = 1\]

\[8,5a = 8,5\]

\[a = 1.\]

\[a = 1 \Longrightarrow b = 2,5 - 1,5 \bullet 1 =\]

\[= 2,5 - 2,2 = 1.\]

\[\frac{1}{x} = 1 \Longrightarrow x = 1.\]

\[\frac{1}{y + 2} = 1\]

\[y + 2 = 1\]

\[y = - 1\]

\[Ответ:(1;\ - 1).\]