Решите систему неравенств: x+6>=13/(x-8); x-1<=56/x.

\[\left\{ \begin{matrix} x + 6^{\backslash x - 8} \geq \frac{13}{x - 8} \\ x - 1^{\backslash x} \leq \frac{56}{x}\text{\ \ \ \ \ \ \ \ \ \ } \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} \frac{(x + 6)(x - 8) - 13}{x - 8} \geq 0 \\ \frac{(x - 6)x - 56}{x} \leq 0\ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} \frac{x^{2} - 2x - 48 - 13}{x - 8} \geq 0 \\ \frac{x^{2} - x - 56}{x} \leq 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ }\]

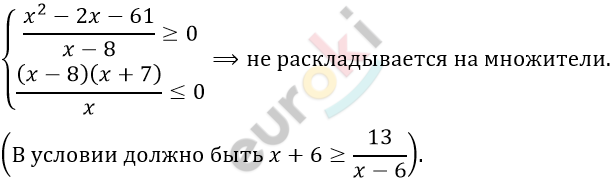
\[\left\{ \begin{matrix} x + 6^{\backslash x - 6} \geq \frac{13}{x - 6} \\ x - 1^{\backslash x} \geq \frac{56}{x}\text{\ \ \ \ \ \ \ \ \ } \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} \frac{(x + 6)(x - 6) - 13}{x - 8} \geq 0 \\ \frac{(x - 6)x - 56}{x} \leq 0\ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \text{\ \ \ \ }\]

\[\left\{ \begin{matrix} \frac{x^{2} - 36 - 13}{x - 6} \geq 0 \\ \frac{x^{2} - x - 56}{x} \leq 0\ \ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} \frac{x^{2} - 49}{x - 6} \geq 0\ \ \ \ \ \ \ \ \ \ \ \ \ \\ \frac{(x - 8)(x + 7)}{x} \leq 0 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} \frac{(x - 7)(x + 7)}{x - 6} \geq 0 \\ \frac{(x - 8)(x + 7)}{x} \leq 0 \\ \end{matrix} \right.\ \]

\[x^{2} - x - 56 =\]

\[= x^{2} - 8x + 7x - 56 =\]

\[= x(x - 8) + 7(x - 8) =\]

\[= (x - 8)(x + 7)\]

\[Ответ:\left\{ - 7 \right\} \cup (0;6) \cup \lbrack 7;8\rbrack.\]