Решите систему неравенств: 5x-4<0; 13/(9x^2-16)<0.

\[\left\{ \begin{matrix} 5x - 4 < 0\ \ \ \ \ \\ \frac{13}{9x^{2} - 16} < 0 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} 5 \cdot (x - 0,8) < 0\ \ \ \ \ \ \ \ \ \ \\ \frac{13}{(3x - 4)(3x + 4)} < 0 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} 5 \cdot (x - 0,8) < 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \frac{13}{9 \cdot \left( x - 1\frac{1}{3} \right)\left( x + 1\frac{1}{3} \right)} < 0 \\ \end{matrix} \right.\ \]

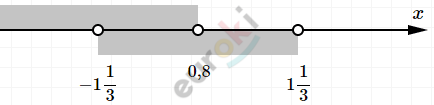
\[Ответ:\left( - 1\frac{1}{3};0,8 \right).\]