Решите систему неравенств: 3-2x<1; 1,6+x<2,9

Ответ:

\[\ \left\{ \begin{matrix} 3 - 2x < 1\ \ \ \ \ \\ 1,6 + x < 2,9 \\ \end{matrix} \right.\ \text{\ \ \ \ \ }\left\{ \begin{matrix} - 2x < - 2 \\ x < 1,3\ \ \ \ \ \\ \end{matrix} \right.\ \text{\ \ \ \ }\left\{ \begin{matrix} x > 1\ \ \ \\ x < 1,3 \\ \end{matrix} \right.\ \]

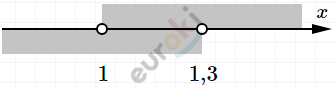
\[Ответ:\ \ \ 1 < x < 1,3.\]

\[\left\{ \begin{matrix} 6 - 2x < 3 \cdot (x - 1) \\ 6 - \frac{x}{2} \geq x\text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } \\ \end{matrix}\text{\ \ \ \ \ \ \ \ } \right.\ \]

\[\left\{ \begin{matrix} 6 - 2x < 3x - 3 \\ 6 \geq x + \frac{x}{2}\text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ } \\ \end{matrix}\text{\ \ \ \ \ \ } \right.\ \]

\[\left\{ \begin{matrix} - 5x < - 9 \\ 6 \geq 1,5x\ \ \ \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} x > \frac{9}{5} \\ x \leq 4 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ }\left\{ \begin{matrix} x > 1,8 \\ x \leq 4\ \ \ \ \\ \end{matrix} \right.\ \]

\[x \in (1,8;4\rbrack.\]

\[Ответ:\ \ x = 2;\ 3;\ 4.\]

\[\sqrt{3x - 2} + \sqrt{6 - x}\]

\[\left\{ \begin{matrix} 3x - 2 \geq 0 \\ 6 - x \geq 0\ \ \\ \end{matrix}\text{\ \ \ \ \ \ \ \ } \right.\ \left\{ \begin{matrix} 3x \geq 2\ \ \ \ \\ - x \geq - 6 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ }\left\{ \begin{matrix} x \geq \frac{2}{3} \\ x \leq 6 \\ \end{matrix} \right.\ \]

\[Ответ:выражение\ имеет\ смысл\ при\ \ \]

\[\frac{2}{3} \leq x \leq 6.\]

\[3x - 7 < \frac{a}{3}\ \ \ \ и\ \ \ x \in ( - \infty;\ \ 4)\]

\[3x < \frac{a}{3} + 7\]

\[3x < \frac{a + 21}{3}\]

\[x < \frac{a + 21}{9}\]

\[- \infty < \frac{a + 21}{9} < 4\]

\[- \infty < a + 21 < 36\]

\[- \infty < a < 15\]

\[Ответ:\ \ a \in ( - \infty;15).\]

\[\frac{1}{3}x \geq 2\]

\[x \geq 6.\]