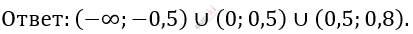Решите систему неравенств: (2x^2-49)/(4x^2-1)>(x-49)/(4x^2-1); (x+1004)/(5x-4)<(x-1003)/(5x-4).

\[\left\{ \begin{matrix} \frac{2x^{2} - 49}{4x^{2} - 1} > \frac{x - 49}{4x^{2} - 1}\text{\ \ \ } \\ \frac{x + 1004}{5x - 4} < \frac{x - 1003}{5x - 4} \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} \frac{2x^{2} - x}{4x^{2} - 1} > 0 \\ \frac{2007}{5x - 4} < 0\ \ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} \frac{x(2x - 1)}{(2x - 1)(2x + 1)} > 0 \\ 5x - 4 < 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} \frac{2x(x - 0,5)}{4 \cdot (x - 0,5)(x + 0,5)} > 0 \\ x < 0,8\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]