Решите неравенство: x(x+3)-6<3(x+1).

Ответ:

\[\ x(x + 3) - 6 < 3 \cdot (x + 1)\]

\[x^{2} + 3x - 6 < 3x + 3\]

\[x^{2} + 3x - 3x - 6 - 3 < 0\]

\[x^{2} - 9 < 0\]

\[x^{2} - 9 = 0\]

\[x^{2} = 9\]

\[x = \pm 3\]

\[Ответ:x \in ( - 3;\ 3).\]

\[\text{\ \ }(x + 8)(x - 3) > 0\]

\[(x + 8)(x - 3) = 0\]

\[x + 8 = 0\ \ \ \ \ \ \ \ x - 3 = 0\]

\[x = - 8\ \ \ \ \ \ \ \ \ \ \ \ x = 3\]

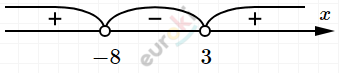
\[Ответ:\ \ \ x \in ( - \infty;\ - 8) \cup (3;\ + \infty).\]