Решите неравенство: x^2-3|x-3|+8<=5|x+2|.

\[x^{2} - 3|x - 3| + 8 \leq 5|x + 2|\]

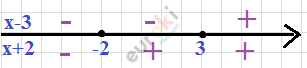
\[1.\ \left\{ \begin{matrix} x < - 2\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ x^{2} + 3x - 9 + 8 \leq - 5x - 10 \\ \end{matrix}\text{\ \ \ \ \ } \right.\ \]

\[\left\{ \begin{matrix} x < - 2\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ x^{2} + 8x + 9 \leq 0 \\ \end{matrix} \right.\ \]

\[x^{2} + 8x + 9 = 0\]

\[D = 64 - 36 = 28\]

\[x_{1,2} = \frac{- 8 \pm 2\sqrt{7}}{2} = - 4 \pm \sqrt{7}\]

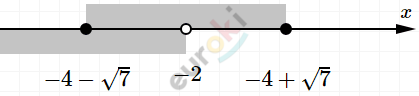
\[\left\lbrack - 4 - \sqrt{7}\ ;\ - 2 \right).\]

\[2.\ \ \left\{ \begin{matrix} - 2 \leq x \leq 3\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ x^{2} + 3x - 9 + 8 \leq 5x + 10 \\ \end{matrix}\text{\ \ \ \ \ \ \ \ } \right.\ \]

\[\left\{ \begin{matrix} - 2 \leq x \leq 3\ \ \ \ \ \ \ \ \ \ \ \\ x^{2} - 2x - 11 \leq 0 \\ \end{matrix} \right.\ \]

\[x^{2} - 2x - 11 = 0\]

\[D = 4 + 44 = 48\]

\[x = \frac{2 \pm 4\sqrt{3}}{2} = 1 \pm 2\sqrt{3}\]

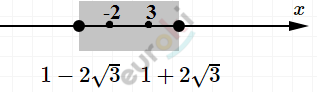
\[\lbrack - 2;3\rbrack\text{.\ }\]

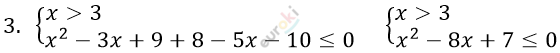
\[x² - 8x + 7 = 0\]

\[x_{1} + x_{2} = 8,\ \ x_{1} \cdot x_{2} = 7\]

\[x = 1,\ \ x = 7\]

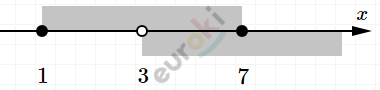
\[(3;7\rbrack.\]

\[Ответ:\left\lbrack - 4 - \sqrt{7};7 \right\rbrack.\]