Решите неравенство: x^2+7x-30>=0.

Ответ:

\[x^{2} + 7x - 30 \geq 0\]

\[x^{2} + 7x - 30 = 0\]

\[x_{1} + x_{2} = - 7\ \ \ \ x_{1} = - 10\]

\[x_{1} \cdot x_{2} = - 30\ \ \ x_{2} = 3\]

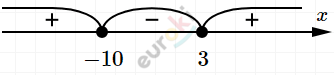
\[Ответ:x \in ( - \infty;\ - 10\rbrack \cup \lbrack 3; + \infty)\]