Решите неравенство методом интервалов: x^3-49x>0.

\[\ x³ - 49x > 0\]

\[x^{3} - 49x = 0\]

\[x(x - 7)(x + 7) = 0\]

\[x = 0\ \ \ \ \ \ \ \ x - 7 = 0\ \ \ \ \ \ x + 7 = 0\]

\[\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x = 7\ \ \ \ \ \ \ \ \ \ \ \ \ \ x = - 7\]

\[Ответ:\ \ x \in ( - 7;0) \cup (7;\ + \infty).\]

\[\sqrt{x^{2} + 4x - 45}\]

\[x^{2} + 4x - 45 \geq 0\]

\[x^{2} + 4x - 45 = 0\]

\[D = b^{2} - 4ac = 16 - 4 \cdot 1 \cdot ( - 45) =\]

\[= 16 + 180 = 196\]

\[x_{1} = \frac{- 4 + 14}{2} = \frac{10}{2} = 5\]

\[x_{2} = \frac{- 4 - 14}{2} = - \frac{18}{2} = - 9\]

\[\mathbf{Ответ:\ }x \in ( - \infty;\ - 9\rbrack \cup \lbrack 5; + \infty).\]

\[\ 3x² + 7x - 6 < 0\]

\[3x^{2} + 7x - 6 = 0\]

\[D = b^{2} - 4ac = 49 - 4 \cdot 3 \cdot ( - 6) =\]

\[= 49 + 72 = 121\]

\[x_{1} = \frac{- 7 + 11}{6} = \frac{4}{6} = \frac{2}{3}\]

\[x_{2} = \frac{- 7 - 11}{6} = - \frac{18}{6} = - 3\]

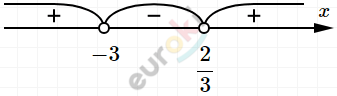
\[Ответ:x \in \left( - 3;\frac{2}{3} \right)\text{.\ }\]