Решите неравенство методом интервалов: x^3-144x>0.

Ответ:

\[\ x³ - 144x > 0\]

\[x(x - 12)(x + 12) = 0\]

\[x = 0\ \ \ \ \ \ \ x - 12 = 0\ \ \ \ \ \ x + 12 = 0\]

\[\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x = 12\ \ \ \ \ \ \ \ \ \ \ \ \ \ x = - 12\]

\[Ответ:\ x \in ( - 12;0) \cup (12; + \infty).\]

\[\sqrt{x^{2} - 3x - 40}\]

\[x^{2} - 3x - 40 \geq 0\]

\[x^{2} - 3x - 40 = 0\]

\[x_{1} + x_{2} = 3\]

\[x_{1} \cdot x_{2} = - 40 \Longrightarrow x_{1} = 8\ \ и\ \ \ x_{2} = - 5\]

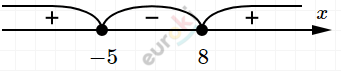
\[Ответ:\ x \in ( - \infty; - 5\rbrack \cup \lbrack 8; + \infty).\]

\[2x^{2} + 7x - 4 > 0\]

\[2x^{2} + 7x - 4 = 0\]

\[D = b^{2} - 4ac = 49 - 4 \cdot 2 \cdot ( - 4) =\]

\[= 49 + 32 = 81\]

\[x_{1} = \frac{- 7 + 9}{4} = \frac{2}{4} = 0,5\]

\[x_{2} = \frac{- 7 - 9}{4} = \frac{- 16}{4} = - 4\]

\[Ответ:\ \ x \in ( - \infty;\ - 4) \cup (0,\ 5;\ + \infty).\]

\[\sqrt{18}\left( \sqrt{6} - \sqrt{2} \right) - 3\sqrt{12} =\]

\[= \sqrt{18 \cdot 6} - \sqrt{18 \cdot 2\ } - 6\sqrt{3} =\]

\[= 6\sqrt{3} - 6 - 6\sqrt{3} = - 6\]

\[\left\{ \begin{matrix} y - 5x = 1\ \ \ \ \ \ \\ y^{2} - 13x = 23 \\ \end{matrix} \right.\ \text{\ \ \ \ \ }\left\{ \begin{matrix} y = 5x + 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ (5x + 1)^{2} - 13x = 23 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} y = 5x + 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ 25x^{2} + 10x + 1 - 1 - 13x = 23 \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} y = 5x + 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ 25x^{2} - 3x - 22 = 0 \\ \end{matrix} \right.\ \text{\ \ \ \ }\]

\[\ \left\lbrack \begin{matrix} \left\{ \begin{matrix} x = 1 \\ y = 6 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ } \\ \left\{ \begin{matrix} x = - \frac{22}{25} \\ y = - 3,4 \\ \end{matrix} \right.\ \\ \end{matrix}\text{\ \ \ \ \ \ \ \ \ \ \ }\left\lbrack \begin{matrix} \left\{ \begin{matrix} x = 1 \\ y = 6 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ } \\ \left\{ \begin{matrix} x = - 0,88 \\ y = - 3,4\ \ \ \\ \end{matrix} \right.\ \\ \end{matrix} \right.\ \right.\ \]

\[25x^{2} - 3x - 22 = 0\]

\[D = b^{2} - 4ac = 9 - 4 \cdot 25 \cdot ( - 22) =\]

\[= 9 + 2200 = 2209\]

\[x_{1} = \frac{3 + 47}{50} = \frac{50}{50} = 1\]

\[x_{2} = \frac{3 - 47}{50} = \frac{- 44}{50} = - \frac{22}{25}\]

\[Ответ:\ \ \ (1;\ \ 6);\ \ \ ( - 0,\ 88;\ - 3,\ 4).\]