Решите неравенство: корень из (4x-3)<=3.

\[\sqrt{4x - 3} \leq 3;\ \ \ \ \ t = 4x - 3\]

\[\sqrt{t} \leq 3 \Longrightarrow 0 \leq t \leq 9 \Longrightarrow\]

\[\Longrightarrow 0 \leq 4x - 3 \leq 9\]

\[\left\{ \begin{matrix} 4x - 3 \geq 0 \\ 4x - 3 \leq 9 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} 4x \geq 3\ \ \\ 4x \leq 12 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} x \geq \frac{3}{4} \\ x \leq 3 \\ \end{matrix} \right.\ \]

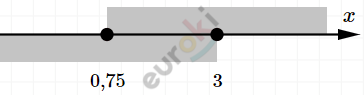
\[Ответ:\lbrack 0,75;3\rbrack.\]