Решите неравенство 2√(x-2)>-3.

Ответ:

\[\sqrt{x - 2} > - 1,5\]

\[x - 2 \geq 0\]

\[x \geq 2.\]

\[\frac{1}{3}a^{2}\sqrt{81a^{6}}\ при\ a < 0:\]

\[\frac{1}{3}a^{2}\sqrt{81a^{6}} = \frac{1}{3}a^{2} \cdot 9\left| a^{3} \right| =\]

\[= 3a^{2} \cdot \left( - a^{3} \right) = - 3a^{5}.\]

\[\frac{2x - 3}{\sqrt{x} - 4}\]

\[x \geq 0;\]

\[\sqrt{x} - 4 \neq 0\]

\[\sqrt{x} \neq 4\]

\[\left( \sqrt{x} \right)^{2} \neq 4^{2}\]

\[x \neq 16.\]

\[\frac{2}{3}\sqrt{196} + 3\sqrt{\frac{81}{289}} - \left( 0,3\sqrt{7} \right)^{2} =\]

\[= \frac{2}{3} \cdot 14 + 3 \cdot \frac{9}{17} - 0,09 \cdot 7 =\]

\[= \frac{28}{3} + \frac{27}{17} - 0,63 =\]

\[= 9\frac{1^{\backslash 1700}}{3} + 1\frac{10^{\backslash 300}}{17} - \frac{63^{\backslash 51}}{100} =\]

\[= 10 + \frac{1700 + 3000 - 3213}{5100} =\]

\[= 10 + \frac{1487}{5100} = 10\ \frac{1487}{5100}\]

\[\frac{\sqrt{392}}{\sqrt{8}} + \sqrt{192} \cdot \sqrt{3} - \sqrt{7^{4} \cdot 5^{2}} =\]

\[= \sqrt{\frac{392}{8}} + \sqrt{64 \cdot 3 \cdot 3} - 7^{2} \cdot 5 =\]

\[= \sqrt{49} + 8 \cdot 3 - 49 \cdot 5 =\]

\[= 7 + 24 - 245 = - 214.\]

\[\sqrt{x^{2} - 4x + 4} = 3\]

\[\sqrt{(x - 2)^{2}} = 3\]

\[|x - 2| = 3\]

\[x - 2 = 3\ \ \ \ \ \ \ \ \ \ \ x - 2 = - 3\]

\[x = 3 + 2\ \ \ \ \ \ \ \ \ \ \ x = - 3 + 2\]

\[x = 5\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x = - 1\]

\[Ответ:x = - 1;x = 5.\]

\[2\sqrt{x - 1} + \sqrt{x} > - 0,2\]

\[x - 1 \geq 0\ \ \ \ \ \ \ \ \ \ \ \ x \geq 0\]

\[x \geq 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \]

\[Ответ:x \geq 1.\]

\[\frac{1}{2}a^{4}\sqrt{36a^{2}} + 2a^{3}\sqrt{9a^{4}}\ при\ a < 0.\]

\[\frac{1}{2}a^{4}\sqrt{36a^{2}} + 2a^{3}\sqrt{9a^{4}} =\]

\[= \frac{1}{2}a^{4} \cdot 6|a| + 2a^{3} \cdot 3\left| a^{2} \right| =\]

\[= 3a^{4} \cdot ( - a) + 6a^{3} \cdot a^{2} =\]

\[= - 3a^{5} + 6a^{5} = 3a^{5}\]

\[\frac{2x - 4}{\sqrt{x - 1} - 2}\]

\[x - 1 \geq 0\]

\[x \geq 1.\]

\[\sqrt{x - 1} - 2 \neq 0\]

\[\sqrt{x - 1} \neq 2\]

\[\left( \sqrt{x - 1} \right)^{2} \neq 2^{2}\]

\[x - 1 \neq 4\]

\[x \neq 5.\]

\[\frac{3}{4}\sqrt{169} + 2\sqrt{\frac{121}{196}} - \left( 0,2\sqrt{6} \right)^{2} =\]

\[= \frac{3}{4} \cdot 13 + 2 \cdot \frac{11}{14} - 0,04 \cdot 6 =\]

\[= \frac{39}{4} + \frac{11}{7} - 0,24 =\]

\[= 9\frac{3^{\backslash 175}}{4} + 1\frac{4^{\backslash 100}}{7} - \frac{6^{\backslash 28}}{25} =\]

\[= 10 + \frac{525 + 400 - 168}{700} =\]

\[= 10 + \frac{757}{700} = 11\frac{57}{700}\]

\[\frac{\sqrt{567}}{\sqrt{7}} + \sqrt{338} \cdot \sqrt{2} - \sqrt{7^{4} \cdot 3^{2}} =\]

\[= \sqrt{\frac{567}{7}\ } + \sqrt{169 \cdot 2 \cdot 2} - 7^{2} \cdot 3 =\]

\[= \sqrt{81} + 13 \cdot 2 - 49 \cdot 3 =\]

\[= 9 + 26 - 147 = - 112.\]

\[\sqrt{x^{2} - 6x + 9} = 4\]

\[\sqrt{(x - 3)^{2}} = 4\]

\[|x - 3| = 4\]

\[x - 3 = 4\ \ \ \ \ \ \ \ \ \ \ x - 3 = - 4\]

\[x = 4 + 3\ \ \ \ \ \ \ \ \ \ \ x = - 4 + 3\]

\[x = 7\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x = - 1\]

\[Ответ:x = - 1;\ \ x = 7.\]

\[3\sqrt{x - 2} + 5\sqrt{x} > - 0,1\]

\[x \geq 0;\]

\[x - 2 \geq 0\]

\[x \geq 2\]

\[Ответ:x \geq 2.\]

\[\frac{1}{3}a^{2}\sqrt{81a^{6}} + 2a\sqrt{16a^{8}}\ при\ a < 0.\]

\[\frac{1}{3}a^{2} \cdot 9\left| a^{3} \right| + 2a \cdot 4\left| a^{4} \right| =\]

\[= 3a^{2} \cdot \left( - a^{3} \right) + 8a \cdot a^{4} =\]

\[= - 3a^{5} + 8a^{5} = 5a^{5}.\]

\[\frac{3x - 6}{\sqrt{x - 2} - 3}\]

\[x - 2 \geq 0\]

\[x \geq 2;\]

\[\sqrt{x - 2} - 3 \neq 0\]

\[\sqrt{x - 2} \neq 3\]

\[\left( \sqrt{x - 2} \right)^{2} \neq 3^{2}\]

\[x - 2 \neq 9\]

\[x \neq 11.\]

\[\sqrt{7 - \sqrt{13}} \cdot \sqrt{\sqrt{13} + 7} =\]

\[= \sqrt{\left( 7 - \sqrt{13} \right)\left( 7 + \sqrt{13} \right)} =\]

\[= \sqrt{7^{2} - \left( \sqrt{13} \right)^{2}} = \sqrt{49 - 13} = \sqrt{36} = 6.\]

\[\sqrt{9 + 4\sqrt{5}} + \left| \sqrt{5} - 4 \right| =\]

\[= \sqrt{\left( \sqrt{5} + 2 \right)^{2}} + \left| \sqrt{5} - 4 \right| =\]

\[= \left| \sqrt{5} + 2 \right| + \left| \sqrt{5} - 4 \right| =\]

\[= \sqrt{5} + 2 - \sqrt{5} + 4 = 6.\]

\[2x + \sqrt{x^{2} - 4x + 4} = 7\]

\[2x + \sqrt{(x - 2)^{2}} = 7\]

\[2x + |x - 2| = 7\]

\[1)\ x - 2 \geq 0:\]

\[|x - 2| = x - 2\]

\[2x + x - 2 = 7\]

\[3x = 9\]

\[x = 3.\]

\[2)\ x - 2 < 0:\]

\[|x - 2| = - x + 2\]

\[2x - x + 2 = 7\]

\[x = 5\ ( > 2)\]

\[нет\ решений.\]

\[Ответ:x = 3.\]

\[2\sqrt{x - 1} + 3\sqrt{x} + 4\sqrt{x + 1} > - 0,1\]

\[x - 1 \geq 0;\ \ \ x \geq 0;\ \ \ x + 1 \geq 0\]

\[x \geq 1;\ \ \ \ x \geq 0;\ \ \ \ x \geq - 1\]

\[Ответ:x \geq 1.\]

\[2a^{4}\sqrt{9a^{2}} + 3a^{3}\sqrt{16a^{4}} + a^{4}|a + 1|\ \]

\[при\ a < 0:\]

\[2a^{4}\sqrt{9a^{2}} + 3a^{3}\sqrt{16a^{4}} + a^{4}|a + 1| =\]

\[= 2a^{4}|3a| + 3a^{3}\left| 4a^{2} \right| + a^{4}|a + 1| =\]

\[= 2a^{4} \cdot ( - 3a) + 3a^{3} \cdot 4a^{2} + a^{4}|a + 1| =\]

\[= - 6a^{2} + 12a^{5} + a^{4}|a + 1| =\]

\[= 6a^{5} + a^{4}|a + 1|\]

\[1)\ a + 1 < 0;\ \ \ \]

\[a < - 1:\]

\[|a + 1| = - (a + 1)\]

\[6a^{5} + a^{4}|a + 1| = 6a^{5} - a^{4}(a + 1) =\]

\[= 6a^{5} - a^{5} - a^{4} = 5a^{5} - a^{4}.\]

\[2)\ a + 1 \geq 0;\ \ a \geq - 1;\]

\[- 1 \leq a < 0:\]

\[|a + 1| = a + 1\]

\[6a^{5} + a^{4}(a + 1) = 6a^{5} + a^{5} + a^{4} =\]

\[= 7a^{5} + a^{4}.\]

\[\frac{3x - 6}{\sqrt{x - 1} - 2} + \frac{5x - 15}{|x| - 2}\]

\[1)\ x - 1 \geq 0\]

\[x \geq 1.\]

\[\sqrt{x - 1} - 2 \neq 0\]

\[\left( \sqrt{x - 1} \right)^{2} \neq 2^{2}\]

\[x - 1 \neq 4\]

\[x \neq 5.\]

\[2)\ |x| - 2 \neq 0\]

\[x \neq 2;\ \ \ x \neq - 2.\]

\[Ответ:x \geq 1;\ \ x \neq 5;\ \ x \neq 2.\]

\[\sqrt{9 - \sqrt{32}} \cdot \sqrt{\sqrt{32} + 9} =\]

\[= \sqrt{(9 - \sqrt{32})(9 + \sqrt{32}} =\]

\[= \sqrt{9^{2} - \left( \sqrt{32} \right)^{2}} = \sqrt{81 - 32} = \sqrt{49} = 7\]

\[7 + 4\sqrt{3} = 4 + 2 \cdot 2\sqrt{3} + 3 = \left( 2 + \sqrt{3} \right)^{2}\]

\[\sqrt{7 + 4\sqrt{3}} + \left| \sqrt{3} - 3 \right| =\]

\[= \sqrt{\left( 2 + \sqrt{3} \right)^{2}} + \left| \sqrt{3} - 3 \right| =\]

\[= \left| 2 + \sqrt{3} \right| + \left| \sqrt{3} - 3 \right| =\]

\[= 2 + \sqrt{3} - \sqrt{3} + 3 = 5\]

\[3x + \sqrt{x^{2} - 6x + 9} = 5\]

\[3x + \sqrt{(x - 3)^{2}} = 5\]

\[3x + |x - 3| = 5\]

\[1)\ x - 3 \geq 0;\ \]

\[\ x \geq 3:\]

\[|x - 3| = x - 3\]

\[3x + x - 3 = 5\]

\[4x = 8\]

\[x = 2\ (но\ x \geq 3)\]

\[нет\ решений.\]

\[2)\ x - 3 < 0;\ \ \]

\[x < 3:\]

\[|x - 3| = - (x - 3) = - x + 3\]

\[3x - x + 3 = 5\]

\[2x = 2\]

\[x = 1\ ( < 3)\]

\[Ответ:x = 1.\]

\[3\sqrt{x - 2} + 2\sqrt{x} + \sqrt{x + 2} > - 0,2\]

\[x - 2 \geq 0;\ \ x \geq 0;\ \ x + 2 \geq 0\]

\[x \geq 2;\ \ \ \ x \geq 0;\ \ \ x \geq - 2.\]

\[Ответ:x \geq 2.\]

\[3a^{2}\sqrt{81a^{6}} + 4a\sqrt{16a^{8}} + a^{4}|a + 2|\ \]

\[при\ a < 0:\]

\[3a^{2}\sqrt{81a^{6}} + 4a\sqrt{16a^{8}} + a^{4}|a + 2| = \ \]

\[= 3a^{2}\left| 9a^{3} \right| + 4a\left| 4a^{4} \right| + a^{4}|a + 2| =\]

\[= 3a^{2} \cdot \left( - 9a^{3} \right) + 4a \cdot 4a^{4} + a^{4}|a + 2| =\]

\[= - 27a^{5} + 16a^{5} + a^{4}|a + 2| =\]

\[= - 11a^{5} + a^{4}|a + 2|\]

\[1)\ a + 2 < 0;\]

\[a < - 2:\]

\[|a + 2| = - (a + 2)\]

\[- 11a^{5} - a^{4}(a + 2) =\]

\[= - 11a^{5} - a^{5} - 2a^{4} = - 12a^{5} - 2a^{4}.\]

\[2)\ a + 2 \geq 0;\]

\[a \geq - 2;\]

\[- 2 \leq a < 0:\]

\[|a + 2| = a + 2\]

\[- 11a^{5} + a^{4}(a + 2) =\]

\[= - 11a^{5} + a^{5} + 2a^{4} = - 10a^{5} + 2a^{4}.\]

\[\frac{2x - 4}{\sqrt{x - 2} - 3} + \frac{4x - 8}{|x| - 4}\]

\[x - 2 \geq 0\]

\[x \geq 2.\]

\[1)\ \sqrt{x - 2} - 3 \neq 0\]

\[\left( \sqrt{x - 2} \right)^{2} \neq 3^{2}\]

\[x - 2 \neq 9\]

\[x \neq 11.\]

\[2)\ |x| - 4 \neq 0\]

\[x \neq \pm 4.\]

\[Ответ:x \geq 2;x \neq 11;x \neq 4.\]

\[\left( 2\sqrt{3} - \sqrt{2} \right)^{2} = 4 \cdot 3 - 2 \cdot 2\sqrt{3} \cdot \sqrt{2} + 2 =\]

\[= 12 - 4\sqrt{6} + 2 = 14 - 4\sqrt{6}\]

\[A = \frac{2}{7}\sqrt{7}\ \ и\ B = \frac{1}{4}\sqrt{20}.\]

\[A = \sqrt{\frac{4}{49} \cdot 7} = \sqrt{\frac{4}{7}}\]

\[B = \sqrt{\frac{1}{16} \cdot 20} = \sqrt{\frac{5}{4}}\]

\[\sqrt{\frac{5}{4}} > \sqrt{\frac{4}{7}}\]

\[A < B.\]

\[\frac{9 - a}{\sqrt{a} - 3\ } = \frac{- (\sqrt{a} - 3)(\sqrt{a} + 3)}{\sqrt{a} - 3} = - \sqrt{a} - 3\]

\[\frac{3\sqrt{2}}{\sqrt{5} - \sqrt{2}} = \frac{3\sqrt{2}\left( \sqrt{5} + \sqrt{2} \right)}{\left( \sqrt{5} - \sqrt{2} \right)\left( \sqrt{5} + \sqrt{2} \right)} =\]

\[= \frac{3\sqrt{10} + 3 \cdot 2}{5 - 2} = \frac{3 \cdot \left( \sqrt{10} + 2 \right)}{3} =\]

\[= 2 + \sqrt{10}\]

\[\frac{1^{\backslash 2\sqrt{3} - 1\ }}{2\sqrt{3} + 1} - \frac{1^{\backslash 2\sqrt{3} + 1}}{2\sqrt{3} - 1\ } =\]

\[= \frac{2\sqrt{3} - 1 - 2\sqrt{3} - 1}{\left( 2\sqrt{3} + 1 \right)\left( 2\sqrt{3} - 1 \right)} = \frac{- 2}{4 \cdot 3 - 1} = - \frac{2}{11}.\]

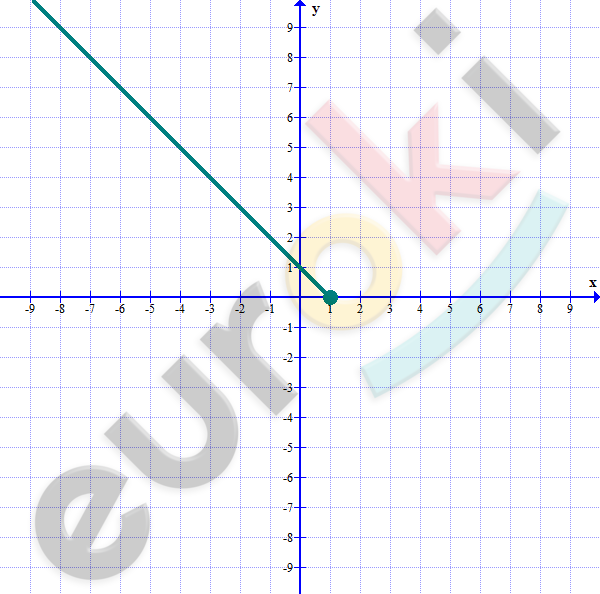
\[y = \left( \sqrt{1 - x} \right)^{2} = 1 - x\]

\[1 - x \geq 0\]

\[x \leq 1.\]

\[\left( 3\sqrt{2} - \sqrt{3} \right)^{2} = 9 \cdot 2 - 2 \cdot 3 \cdot \sqrt{2} \cdot \sqrt{3} + 3 =\]

\[= 18 - 6\sqrt{6} + 3 = 21 - 6\sqrt{6}\]

\[A = \frac{3}{5}\sqrt{20}\ и\ B = \frac{2}{3}\sqrt{12}\]

\[A = \sqrt{\frac{9}{25} \cdot 20} = \sqrt{\frac{36}{5}} = \sqrt{7\frac{1}{5}}\]

\[B = \sqrt{\frac{4}{9} \cdot 12} = \sqrt{\frac{16}{3}} = \sqrt{5\frac{1}{3}}\]

\[\sqrt{7\frac{1}{5}} > \sqrt{5\frac{1}{3}}\]

\[A > B.\]

\[\frac{16 - c}{\sqrt{c} - 4} = \frac{- \left( \sqrt{c} - 4 \right)\left( \sqrt{c} + 4 \right)}{\sqrt{c} - 4} = - \sqrt{c} - 4\]

\[\frac{2\sqrt{5}}{\sqrt{5} - \sqrt{3}} = \frac{2\sqrt{5}\left( \sqrt{5} + \sqrt{3} \right)}{\left( \sqrt{5} - \sqrt{3} \right)\left( \sqrt{5} + \sqrt{3} \right)} =\]

\[= \frac{2 \cdot 5 + 2\sqrt{5} \cdot \sqrt{3}}{5 - 3} = \frac{2\left( 5 + \sqrt{15} \right)}{2} =\]

\[= 5 + \sqrt{15}\]

\[\frac{1^{\backslash 1 - 3\sqrt{5}}}{1 + 3\sqrt{5}} + \frac{1^{\backslash 1 + 3\sqrt{5}}}{1 - 3\sqrt{5}} =\]

\[= \frac{1 - 3\sqrt{5} + 1 + 3\sqrt{5}}{\left( 1 + 3\sqrt{5} \right)\left( 1 - 3\sqrt{5} \right)} = \frac{2}{1 - 9 \cdot 5} =\]

\[= \frac{2}{- 44} = - \frac{1}{22}.\]

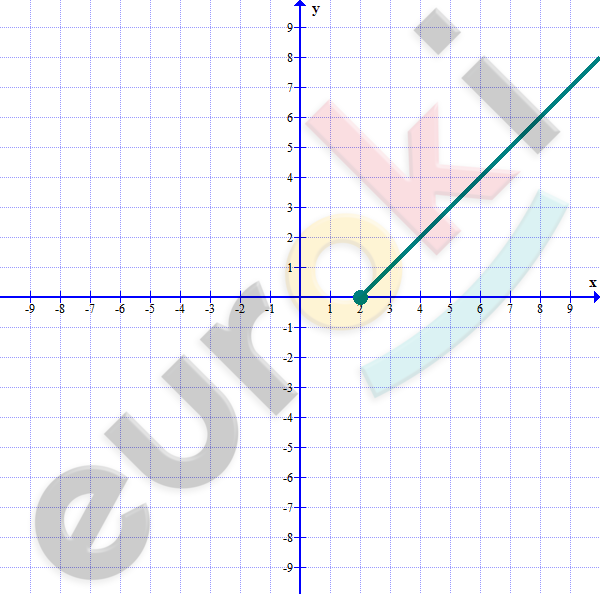
\[y = \left( \sqrt{x - 2} \right)^{2} = x - 2\]

\[x - 2 \geq 0\]

\[x \geq 2.\]

\[2\sqrt{18} + 5\sqrt{50} - \frac{1}{4}\sqrt{32} - 7\sqrt{2} =\]

\[= 2\sqrt{9 \cdot 2} + 5\sqrt{25 \cdot 2} - \frac{1}{4}\sqrt{16 \cdot 2} - 7\sqrt{2} =\]

\[= 6\sqrt{2} + 25\sqrt{2} - \sqrt{2} - 7\sqrt{2} = 23\sqrt{2}\]

\[\left( 2\sqrt{3} - 1 \right)\left( 3\sqrt{3} + 5 \right) - 7\sqrt{3} =\]

\[= 6 \cdot 3 - 3\sqrt{3} + 10\sqrt{3} - 5 - 7\sqrt{3} = 13\]

\[\frac{6\sqrt{3}}{3\sqrt{2} - 2\sqrt{3}} = \frac{6\sqrt{3}\left( 3\sqrt{2} + 2\sqrt{3} \right)}{\left( 3\sqrt{2} - 2\sqrt{3} \right)\left( 3\sqrt{2} + 2\sqrt{3} \right)} =\]

\[= \frac{18\sqrt{6} + 12 \cdot 3}{9 \cdot 2 - 4 \cdot 3} = \frac{18\sqrt{6} + 36}{18 - 12} =\]

\[= \frac{6\left( 3\sqrt{6} + 6 \right)}{6} = 6 + 3\sqrt{6}\]

\[\frac{a^{2} + 2a\sqrt{b} + b}{a + \sqrt{b}} = \frac{\left( a + \sqrt{b} \right)^{2}}{a + \sqrt{b}} = a + \sqrt{b}.\]

\[A = \sqrt{20} - \sqrt{18}\ и\ B = \sqrt{14} - \sqrt{12}\]

\[A^{2} = \left( \sqrt{20} - \sqrt{18} \right)^{2} =\]

\[= 20 - 2\sqrt{360} + 18 = 38 - 2 \cdot 60 =\]

\[= 38 - 120 = - 82 < 0\]

\[B^{2} = \left( \sqrt{14} - \sqrt{12} \right)^{2} = 14 - 2\sqrt{168} + 12 =\]

\[= 26 - 2\sqrt{168} > 0\]

\[A < B.\]

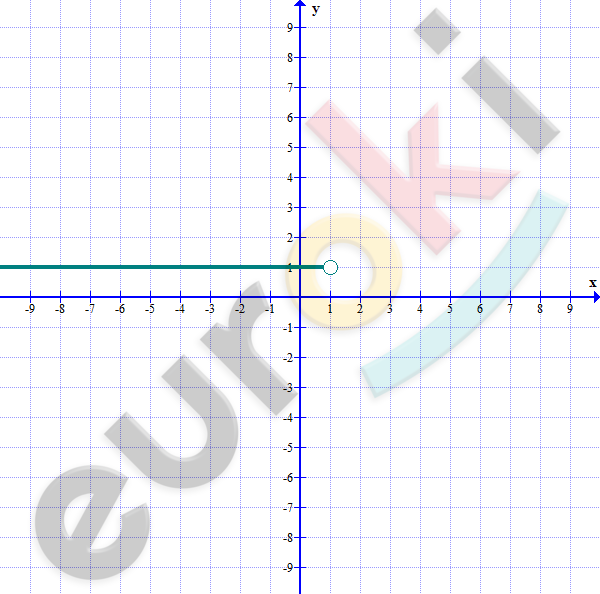
\[y = \frac{\left( \sqrt{1 - x} \right)^{2}}{|x - 1|} = \frac{1 - x}{1 - x} = 1\]

\[1 - x < 0\]

\[- x < - 1\]

\[x < 1.\]

\[2\sqrt{27} + 4\sqrt{48} - \frac{1}{5}\sqrt{75} - 9\sqrt{3} =\]

\[= 2\sqrt{3 \cdot 9} + 4\sqrt{3 \cdot 16} - \frac{1}{5}\sqrt{3 \cdot 25} - 9\sqrt{3} =\]

\[= 6\sqrt{3} + 16\sqrt{3} - \sqrt{3} - 9\sqrt{3} = 12\sqrt{3}\]

\[\left( 3\sqrt{2} - 2 \right)\left( 4\sqrt{2} + 7 \right) - 13\sqrt{2} =\]

\[= 12 \cdot 2 - 8\sqrt{2} + 21\sqrt{2} - 14 - 13\sqrt{2} = 10.\]

\[\frac{2\sqrt{5}}{2\sqrt{5} - 3\sqrt{2}} = \frac{2\sqrt{5}\left( 2\sqrt{5} + 3\sqrt{2} \right)}{\left( 2\sqrt{5} - 3\sqrt{2} \right)\left( 2\sqrt{5} + 3\sqrt{2} \right)} =\]

\[= \frac{4 \cdot 5 + 6\sqrt{5} \cdot \sqrt{2}}{4 \cdot 5 - 9 \cdot 2} = \frac{20 + 6\sqrt{10}}{20 - 18} =\]

\[= \frac{2\left( 10 + 3\sqrt{10} \right)}{2} = 10 + 3\sqrt{10}\]

\[\frac{4x^{2} - 4x\sqrt{y} + y}{2x - \sqrt{y}} = \frac{\left( 2x - \sqrt{y} \right)^{2}}{2x - \sqrt{y}} =\]

\[= 2x - \sqrt{y}\]

\[A = \sqrt{32} - \sqrt{31}\ и\ B = \sqrt{43} - \sqrt{42}\]

\[A^{2} = \left( \sqrt{32} - \sqrt{31} \right)^{2} =\]

\[= 32 - 2\sqrt{32 \cdot 31} + 31 = 63 - 2\sqrt{32 \cdot 31}\]

\[B^{2} = \left( \sqrt{43} - \sqrt{42} \right)^{2} =\]

\[= 43 - 2\sqrt{43 \cdot 42} + 42 = 85 - 2\sqrt{43 \cdot 42}\]

\[A > B.\]

\[y = \frac{\left( \sqrt{x - 2} \right)^{2}}{|x - 2|} = \frac{x - 2}{x - 2} = 1\]

\[x - 2 > 0\]

\[x > 2.\]

\[\left( 2\sqrt{3} + 5 \right)^{2} + \left( 10 - \sqrt{3} \right)^{2} =\]

\[= 4 \cdot 3 + 20\sqrt{3} + 25 + 100 - 20\sqrt{3} + 3 =\]

\[= 12 + 128 = 140.\]

\[\frac{a + \sqrt{a}}{1 + \sqrt{a}} + \frac{a - 1}{1 + \sqrt{a}} - 2\sqrt{a} =\]

\[= \frac{\sqrt{a}\left( \sqrt{a} + 1 \right)}{1 + \sqrt{a}} + \frac{\left( \sqrt{a} - 1 \right)\left( \sqrt{a} + 1 \right)}{1 + \sqrt{a}} - 2\sqrt{a} =\]

\[= \sqrt{a} + \sqrt{a} - 1 - 2\sqrt{a} = - 1.\]

\[\sqrt{\left( 12 - \sqrt{13} \right)^{2}} + \sqrt{\left( 3 - \sqrt{13} \right)^{2}} =\]

\[= \left| 12 - \sqrt{13} \right| + \left| 3 - \sqrt{13} \right| =\]

\[= 12 - \sqrt{13} + \sqrt{13} - 3 = 9.\]

\[y = \sqrt{x^{2} - 4x + 4} + x = \sqrt{(x - 2)^{2}} + x =\]

\[= |x - 2| + x\]

\[1)\ x < 2:\]

\[y = 2 - x + x = 2;\]

\[2)\ x \geq 2:\]

\[y = x - 2 + x = 2x - 2.\]

\[A = \sqrt{3} + \sqrt{2}\ и\ B = \sqrt{10}\]

\[A^{2} = \left( \sqrt{3} + \sqrt{2} \right)^{2} = 3 + 2\sqrt{6} + 2 = 5 + 2\sqrt{6}\]

\[B^{2} = \left( \sqrt{10} \right)^{2} = 5 + 5\]

\[2\sqrt{6} < 5\]

\[A < B.\]

\[\sqrt{28 - a} - \sqrt{13 - a} = 3\]

\[Умножим\ обе\ части\ равенства\ на\ \]

\[\sqrt{28 - a} + \sqrt{13 - a}.\]

\[1)\ \left( \sqrt{28 - a} - \sqrt{13 - a} \right)\left( \sqrt{28 - a} + \sqrt{13 - a} \right) =\]

\[= 28 - a - (13 - a) =\]

\[= 28 - a - 13 + a = 15.\]

\[2)\ 3\left( \sqrt{28 - a} + \sqrt{13 - a} \right) = 15\]

\[\sqrt{28 - a} + \sqrt{13 - a} = 5.\]

\[Ответ:5.\]

\[\left( 3\sqrt{2} + 2 \right)^{2} + \left( 6 - \sqrt{2} \right)^{2} =\]

\[= 9 \cdot 2 + 12\sqrt{2} + 4 + 36 - 12\sqrt{2} + 2 =\]

\[= 18 + 42 = 60\]

\[\frac{a - 2\sqrt{a} + 1}{1 - \sqrt{a}} + \frac{a - 1}{1 - \sqrt{a}} + 2\sqrt{a} =\]

\[= \frac{\left( 1 - \sqrt{a} \right)^{2}}{1 - \sqrt{a}} - \frac{\left( 1 - \sqrt{a} \right)\left( 1 + \sqrt{a} \right)}{1 - \sqrt{a}} + 2\sqrt{a} =\]

\[= 1 - \sqrt{a} - 1 - \sqrt{a} + 2\sqrt{a} = 0.\]

\[\sqrt{\left( 15 - \sqrt{11} \right)^{2}} + \sqrt{\left( 2 - \sqrt{11} \right)^{2}} =\]

\[= \left| 15 - \sqrt{11} \right| + \left| 2 - \sqrt{11} \right| =\]

\[= 15 - \sqrt{11} + \sqrt{11} - 2 = 13.\]

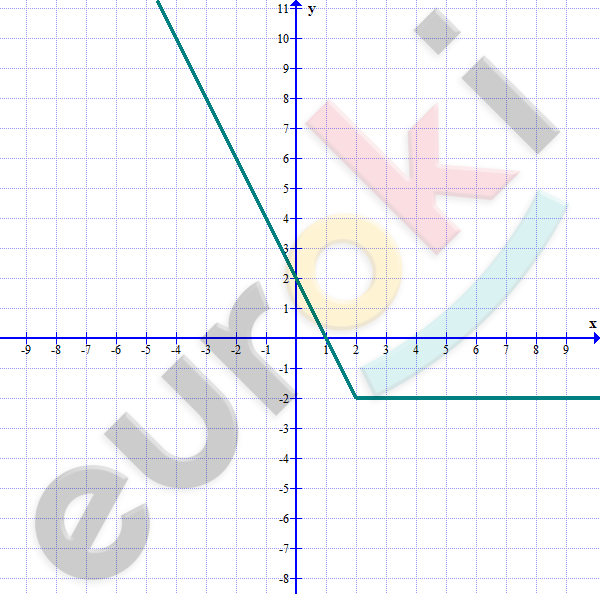
\[y = \sqrt{x^{2} - 4x + 4} - x = \sqrt{(x - 2)^{2}} - x =\]

\[= |x - 2| - x\]

\[1)\ x < 2:\]

\[y = 2 - x - x = 2 - 2x.\]

\[2)\ x \geq 2:\]

\[y = x - 2 - x = - 2.\]

\[A = \sqrt{2} + \sqrt{5}\ и\ B = \sqrt{13}.\]

\[A^{2} = \left( \sqrt{2} + \sqrt{5} \right)^{2} = 2 + 2\sqrt{10} + 5 =\]

\[= 7 + 2\sqrt{10};\ \ (2\sqrt{10} > 6)\]

\[B^{2} = \left( \sqrt{13} \right)^{2} = 13 = 7 + 6\]

\[A > B.\]

\[\sqrt{39 - a} + \sqrt{27 - a} = 4\]

\[Умножим\ обе\ части\ равенства\ на\ \]

\[\sqrt{39 - a} - \sqrt{27 - a}:\]

\[\left( \sqrt{39 - a} + \sqrt{27 - a} \right)\left( \sqrt{39 - a} - \sqrt{27 - a} \right) =\]

\[= 39 - a - (27 - a) =\]

\[= 39 - a - 27 + a = 12\]

\[4 \cdot \left( \sqrt{39 - a} - \sqrt{27 - a} \right) = 12\]

\[\sqrt{39 - a} - \sqrt{27 - a} = 3.\]

\[5x^{2} + 10x = 0\]

\[5x(x + 2) = 0\]

\[5x = 0\ \ \ \ \ \ x + 2 = 0\]

\[x = 0\ \ \ \ \ \ \ \ x = - 2\]

\[Ответ:x = 0;\ \ x = - 2.\]

\[9x^{2} - 4 = 0\]

\[(3x - 2)(3x + 2) = 0\]

\[3x - 2 = 0\ \ \ \ \ \ \ 3x + 2 = 0\]

\[3x = 2\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 3x = - 2\]

\[x = \frac{2}{3}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x = - \frac{2}{3}\]

\[Ответ:x = \pm \frac{2}{3}.\]

\[x^{2} - 7x + 6 = 0\]

\[По\ теореме\ Виета:\]

\[x_{1} + x_{2} = 7;\ \ \ x_{1} \cdot x_{2} = 6\]

\[x_{1} = 1;\ \ \ \ x_{2} = 7\]

\[Ответ:x = 1;x = 7.\]

\[2x^{2} + 3x + 4 = 0\]

\[D = 9 - 32 = - 23 < 0\]

\[нет\ корней.\]

\[Ответ:нет\ корней.\]

\[x^{2} + ax + 72 = 0;\ \ \ x_{1} = 9\]

\[x_{1} \cdot x_{2} = 72\]

\[x_{2} = 72\ :9 = 8.\]

\[- a = 8 + 9 = 17\]

\[a = - 17.\]

\[Ответ:x_{2} = 8;\ \ a = - 17.\]

\[P = 2 \cdot (a + b) = 26\]

\[a + b = 13.\]

\[Пусть\ \text{a\ }см - одна\ сторона\ \]

\[прямоугольника,\ (13 - a)\ см -\]

\[другая\ сторона.\]

\[Площадь\ равна\ 36\ см^{2}.\]

\[Составим\ уравнение:\]

\[a(13 - a) = 36\]

\[13a - a^{2} - 36 = 0\]

\[a^{2} - 13a + 36 = 0\]

\[D = 169 - 144 = 25\]

\[a_{1} = \frac{13 - 5}{2} = 4\ (см) - одна\ сторона.\]

\[13 - a = 13 - 4 = 9\ (см) - другая\ \]

\[сторона.\]

\[a_{2} = \frac{13 + 5}{2} = 9\ (см) - одна\ сторона.\]

\[13 - a = 13 - 9 = 4\ (см) - другая\]

\[сторона.\]

\[Ответ:4\ см\ и\ 9\ см.\]

\[6x^{2} + 18x = 0\]

\[6x(x + 3) = 0\]

\[6x = 0\ \ \ \ \ x + 3 = 0\]

\[x = 0\ \ \ \ \ \ \ x = - 3\]

\[Ответ:x = - 3;\ \ x = 0.\]

\[4x^{2} - 9 = 0\]

\[(2x - 3)(2x + 3) = 0\]

\[2x - 3 = 0\ \ \ \ \ \ 2x + 3 = 0\]

\[2x = 3\ \ \ \ \ \ \ \ \ \ \ \ \ \ 2x = - 3\]

\[x = 1,5\ \ \ \ \ \ \ \ \ \ \ \ \ x = - 1,5\]

\[Ответ:x = \pm 1,5.\]

\[x^{2} - 8x + 7 = 0\]

\[По\ теореме\ Виета:\]

\[x_{1} + x_{2} = 8;\ \ \ \ x_{1} \cdot x_{2} = 7\]

\[x_{1} = 1;\ \ \ x_{2} = 7.\]

\[Ответ:x = 1;\ \ x = 7.\]

\[3x^{2} + 5x + 6 = 0\]

\[D = 25 - 72 = - 47 < 0\]

\[нет\ корней.\]

\[Ответ:нет\ корней.\]

\[x^{2} + 11x + a = 0;\ \ x_{1} = 3\]

\[x_{1} + x_{2} = - 11\]

\[x_{2} = - 11 - 3 = - 14.\]

\[a = x_{1} \cdot x_{2}\]

\[a = 3 \cdot ( - 14) = - 42.\]

\[Ответ:x_{2} = - 14;\ \ a = - 42.\]

\[P = 2 \cdot (a + b) = 22\]

\[a + b = 11\]

\[Пусть\ \text{a\ }см - одна\ сторона\ \]

\[прямоугольника,\ (11 - a)\ см - другая\]

\[сторона.\]

\[Площадь\ равна\ 24\ см^{2}.\]

\[Составим\ уравнение:\]

\[a(11 - a) = 24\]

\[11a - a^{2} - 24 = 0\]

\[a^{2} - 11a + 24 = 0\]

\[D = 121 - 96 = 25\]

\[a_{1} = \frac{11 + 5}{2} = 8\ (см) - одна\ сторона.\]

\[11 - a = 11 - 8 = 3\ (см) - другая\ \]

\[сторона\ прямоугольника.\]

\[{a_{2} = \frac{11 - 5}{2} = 3\ (см) - одна\ сторона. }{11 - a = 11 - 3 = 8\ (см) - другая\ }\]

\[сторона.\]

\[Ответ:3\ см\ и\ 8\ см.\]

\[2x^{2} - 7x + 5 = 0\]

\[D = 49 - 40 = 9\]

\[x_{1} = \frac{7 + 9}{4} = 4;\ \ \ \]

\[x_{2} = \frac{7 - 9}{4} = - \frac{2}{4} = - 0,5\]

\[Ответ:x = - 0,5;\ \ x = 4.\]

\[(2x - 1)^{2} - 9 = 0\]

\[(2x - 1)^{2} = 9\]

\[2x - 1 = 3\ \ \ \ \ \ \ \ \ \ 2x - 1 = - 3\]

\[2x = 4\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 2x = - 2\]

\[x = 2\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x = - 1\]

\[Ответ:x = - 1;\ \ x = 2.\]

\[x^{2} + 2ax - 3a^{2} = 0\]

\[D = 4a^{2} + 4 \cdot 3a^{2} = 16a^{2}\]

\[x_{1} = \frac{- 2a + 4a}{2} = a;\]

\[x_{2} = \frac{- 2a - 4a}{2} = - 3a.\]

\[Ответ:x = - 3a;x = a.\]

\[x_{1} = - 3;\ \ \ x_{2} = \frac{1}{2}\]

\[ax^{2} + bx + c = 0\]

\[b = - \left( - 3 + \frac{1}{2} \right) = - ( - 2,5) = 2,5;\]

\[c = - 3 \cdot \frac{1}{2} = - 1,5.\]

\[x^{2} + 2,5x - 1,5 = 0\ \ \ \ | \cdot 2\]

\[2x^{2} + 5x - 3 = 0\]

\[Ответ:2x^{2} + 5x - 3 = 0.\]

\[Пусть\ x\ \frac{км}{ч} - собственная\ скорость\]

\[катера;\]

\[\frac{30}{x + 3}\ ч - шел\ по\ течению.\]

\[\frac{24}{x - 3}\ \ ч - шел\ против\ течения.\]

\[На\ весь\ путь\ катер\ затратил\ 9\ ч.\]

\[Составим\ уравнение:\]

\[\frac{30^{\backslash x - 3}}{x + 3} + \frac{24^{\backslash x + 3}}{x - 3} = 9^{\backslash x^{2} - 9}\ ;\ \ \ x \neq 3;\ \ x \neq - 3\]

\[\frac{30x - 90 + 24x + 72 - 9x^{2} + 81}{(x + 3)(x - 3)} = 0\]

\[- 9x^{2} + 54x + 63 = 0\ \ \ \ \ |\ :( - 9)\]

\[x^{2} - 6x - 7 = 0\]

\[D = 9 + 7 = 16\]

\[x_{1} = 3 + 4 = 7\ \left( \frac{км}{ч} \right) - собственная\]

\[скорость\ катера.\]

\[x_{2} = 3 - 4 = - 1 < 0 - не\ подходит.\]

\[Ответ:7\ \frac{км}{ч}\text{.\ \ \ }\]

\[x^{2} + px + q = 0\]

\[x_{1} + x_{2} = - p\]

\[x_{1} \cdot x_{2} = q\]

\[\left( x_{1} + x_{2} \right)^{2} = ( - p)^{2}\]

\[x_{1}^{2} + 2x_{1}x_{2} + x_{2}^{2} = p^{2}\]

\[x_{1}^{2} + x_{2}^{2} = p^{2} - 2x_{1}x_{2} = p^{2} - 2q\]

\[Ответ:p^{2} - 2q.\]

\[3x^{2} - 7x + 4 = 0\]

\[D = 49 - 48 = 1\]

\[x_{1} = \frac{7 + 1}{6} = \frac{8}{6} = \frac{4}{3} = 1\frac{1}{3};\]

\[x_{2} = \frac{7 - 1}{6} = 1\]

\[Ответ:x = 1;\ \ x = 1\frac{1}{3}.\]

\[(3x + 1)^{2} - 4 = 0\]

\[(3x + 1)^{2} = 4\]

\[3x + 1 = 2\ \ \ \ \ \ \ 3x + 1 = - 2\]

\[3x = 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 3x = - 3\]

\[x = \frac{1}{3}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x = - 1\]

\[Ответ:x = - 1;\ \ x = \frac{1}{3}.\]

\[x^{2} - 3ax - 4a^{2} = 0\]

\[D = 9a^{2} + 16a^{2} = 25a^{2}\]

\[x_{1} = \frac{3a + 5a}{2} = 4a;\]

\[x_{2} = \frac{3a - 5a}{2} = - a\]

\[Ответ:x = - a;\ x = 4a.\]

\[x_{1} = - 2;\ \ \ x_{2} = \frac{1}{3}\]

\[ax^{2} + bx + c = 0\]

\[b = - \left( - 2 + \frac{1}{3} \right) = - \left( - 1\frac{2}{3} \right) = \frac{5}{3};\]

\[c = - 2 \cdot \frac{1}{3} = - \frac{2}{3}\]

\[x^{2} + \frac{5}{3}x - \frac{2}{3} = 0\ \ \ \ \ | \cdot 3\]

\[3x^{2} + 5x - 2 = 0\]

\[Ответ:3x^{2} + 5x - 2 = 0.\]

\[Пусть\ x\ \frac{км}{ч} - скорость\ лодки\ в\ \]

\[стоячей\ воде.\]

\[\frac{45}{x + 2}\ ч - на\ путь\ по\ течению;\]

\[\frac{22}{x - 2}\ ч - на\ путь\ против\ течения.\]

\[На\ весь\ путь\ лодка\ затратила\ 5\ ч.\]

\[Составим\ уравнение:\]

\[\frac{45}{x + 2} + \frac{22}{x - 2} = 5;\ \ \ \ x \neq \pm 2\]

\[45 \cdot (x - 2) + 22 \cdot (x + 2) = 5 \cdot (x^{2} - 4)\]

\[45x - 90 + 22x + 44 = 5x^{2} - 20\]

\[5x^{2} - 67x + 26 = 0\]

\[D = 4489 - 520 = 3969 = 63^{2}\]

\[x_{1} = \frac{67 + 63}{10} = \frac{130}{10} = 13\ \left( \frac{км}{ч} \right) -\]

\[скорость\ лодки\ в\ стоячей\ воде.\]

\[x_{2} = \frac{67 - 63}{10} = \frac{4}{10} = 0,4 - не\ подходит.\]

\[Ответ:13\ \frac{км}{ч}.\]

\[x^{2} + px + q = 0\]

\[x_{1} + x_{2} = - p\]

\[x_{1} \cdot x_{2} = q\]

\[\frac{1^{\backslash x_{2}}}{x_{1}} + \frac{1^{\backslash x_{1}}}{x_{2}} = \frac{x_{2} + x_{1}}{x_{1} \cdot x_{2}} = \frac{- p}{q}\]

\[Ответ:\ - \frac{p}{q}.\]

\[6x^{2} + x - 2 = 0\]

\[D = 1 + 24 = 25\]

\[x_{1} = \frac{- 1 + 5}{12} = \frac{4}{12} = \frac{1}{3};\]

\[x_{2} = \frac{- 1 - 5}{12} = - \frac{6}{12} = - \frac{1}{2}\]

\[Ответ:x = \frac{1}{3};\ \ x = - 0,5.\]

\[(3x + 1)^{2} = (x + 2)^{2}\]

\[(3x + 1)^{2} - (x + 2)^{2} = 0\]

\[\left( 3x + 1 - (x + 2) \right) \cdot (3x + 1 + x + 2) = 0\]

\[(2x - 1)(4x + 3) = 0\]

\[2x - 1 = 0\ \ \ \ \ \ \ \ \ \ 4x + 3 = 0\]

\[2x = 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 4x = - 3\]

\[{x = 0,5\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x = - 0,75 }{Ответ:x = 0,5;\ \ x = - 0,75.}\]

\[x^{2} - x - a^{2} + a = 0\]

\[D = 1 - 4 \cdot \left( - a^{2} + a \right) =\]

\[= 1 + 4a^{2} - 4a = (2a - 1)^{2}\]

\[x_{1} = \frac{1 - 2a + 1}{2} = \frac{2 - 2a}{2} = 1 - a;\]

\[x_{2} = \frac{1 + 2a - 1}{2} = \frac{2a}{2} = a\]

\[Ответ:x = 1 - a;\ \ x = a.\]

\[Пусть\ x;x + 1;x + 2;x + 3 - четыре\]

\[последовательных\ числа.\]

\[x(x + 3) = x^{2} + 3x - произведение\ \]

\[крайних\ чисел;\]

\[(x + 1)(x + 2) = x^{2} + 3x + 2 -\]

\[произведение\ средних\ чисел.\]

\[Составим\ уравнение:\]

\[x^{2} + 3x + x^{2} + 3x + 2 = 22\]

\[2x^{2} + 6x - 20 = 0\ \ \ \ \ |\ :2\]

\[x^{2} + 3x - 10 = 0\]

\[x_{1} + x_{2} = - 3;\ \ \ x_{1} \cdot x_{2} = - 10\]

\[x_{1} = - 5;\ \ \ \ x_{2} = 2.\]

\[Два\ набора\ чисел:\]

\[1)\ - 5,\ - 4,\ - 3,\ - 2;\]

\[2)\ 2,\ 3,\ 4,\ 5.\]

\[x^{2} + \left( 8a - a^{2} \right)x - a^{4} = 0\]

\[D = \left( 8 - a^{2} \right)^{2} + 4a^{4} \geq 0\ при\ любом\ \text{a.}\]

\[x_{1} + x_{2} = - \left( 8a - a^{2} \right) = a^{2} - 8a =\]

\[= \left( - a^{2} - 8a + 16 \right) - 16 = (a - 4)^{2} - 16\]

\[x_{1} + x_{2} \geq - 16\]

\[Наименьшее\ значение\ суммы\ корней\]

\[равно\ - 16\ при\ a = 4.\]

\[Ответ:\ - 16.\]

\[x^{2} + 3x - 2a^{2} = 0\]

\[D = 9 + 8a^{2} > 0\ при\ любом\ \text{a.}\]

\[x_{1} + x_{2} = - 3;\ \ \ x_{1} \cdot x_{2} = - 2a^{2}\]

\[y^{2} + py + q = 0 - искомое\ уравнение.\]

\[y_{1} + y_{2} = \left( x_{1} + 1 \right) + \left( x_{2} + 1 \right) =\]

\[= \left( x_{1} + x_{2} \right) + 2 = - 3 + 2 = - 1.\]

\[y_{1} \cdot y_{2} = \left( x_{1} + 1 \right)\left( x_{2} + 1 \right) =\]

\[= x_{1}x_{2} + \left( x_{1} + x_{2} \right) + 1 = - 2a^{2} - 3 + 1 =\]

\[= - 2a^{2} - 2\]

\[По\ теореме\ Виета:\]

\[p = - \left( y_{1} + y_{2} \right) = - ( - 1) = 1;\]

\[q = y_{1} \cdot y_{2} = - 2a^{2} - 2.\]

\[Искомое\ уравнение\ имеет\ вид:\]

\[y^{2} + y - 2a^{2} - 2 = 0.\]

\[9x^{2} + 3x - 2 = 0\]

\[D = 9 + 72 = 81\]

\[x_{1} = \frac{- 3 + 9}{18} = \frac{6}{18} = \frac{1}{3};\]

\[x_{2} = \frac{- 3 - 9}{18} = - \frac{12}{18} = - \frac{2}{3}\]

\[Ответ:x = \frac{1}{3};\ \ x = - \frac{2}{3}.\]

\[(4x + 3)^{2} = (2x - 1)^{2}\]

\[(4x + 3)^{2} - (2 - 1)^{2} = 0\]

\[\left( 4x + 3 - (2x - 1) \right)(4x + 3 + 2x - 1) = 0\]

\[(2x + 4)(6x + 2) = 0\]

\[2x + 4 = 0\ \ \ \ \ \ \ \ \ \ \ 6x + 2 = 0\]

\[2x = - 4\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 6x = - 2\]

\[x = - 2\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x = - \frac{1}{3}\]

\[Ответ:x = - 2;\ \ x = - \frac{1}{3}.\]

\[x^{2} + 3x - 4a^{2} + 6a = 0\]

\[D = 9 - 4 \cdot \left( - 4a^{2} + 6a \right) =\]

\[= 9 + 16a^{2} - 24a = (4a - 3)^{2} \geq 0 - при\]

\[любом\ значении\ \text{a.}\]

\[x_{1} = \frac{- 3 + 4a - 3}{2} = \frac{4a - 6}{2} = 2a - 3;\]

\[x_{2} = \frac{- 3 - 4a + 3}{2} = - \frac{4a}{2} = - 2a.\]

\[Ответ:x = 2a - 3;\ \ \ x = - 2a.\]

\[Пусть\ x;x + 1;x + 2;x + 3 - четыре\]

\[последовательных\ числа.\]

\[x(x + 3) = x^{2} + 3x - произведение\ \]

\[крайних\ чисел;\]

\[(x + 1)(x + 2) = x^{2} + 3x + 2 -\]

\[произведение\ средних\ чисел.\]

\[Составим\ уравнение:\]

\[x^{2} + 3x + x^{2} + 3x + 2 = 38\]

\[2x^{2} + 6x - 36 = 0\ \ \ \ |\ :2\]

\[x^{2} + 3x - 18 = 0\]

\[x_{1} + x_{2} = - 3;\ \ \ \ x_{1} \cdot x_{2} = - 18\]

\[x_{1} = - 6;\ \ \ x_{2} = 3\]

\[Два\ набора\ чисел:\]

\[1) - 6;\ - 5;\ - 4;\ - 3.\]

\[2)\ 3;4;5;6.\]

\[x^{2} + \left( a^{2} - 6a \right)x - 3a^{2} = 0\]

\[D = \left( a^{2} - 6a \right)^{2} + 12a^{2} \geq 0\ при\ любом\]

\[значении\ \text{a.}\]

\[x_{1} + x_{2} = - \left( a^{2} - 6a \right) =\]

\[= - \left( a^{2} - 6a + 9 \right) + 9 = - (a - 3)^{2} + 9\]

\[- (a - 3)^{2} \leq 0\ при\ любом\ \text{a.}\]

\[x_{1} + x_{2} \leq 9\]

\[Наименьшее\ значение\ суммы\ корней\ \]

\[равно\ 9\ при\ a = 3.\]

\[Ответ:9.\]

\[x^{2} + 2x - 3a^{2} = 0\]

\[D = 4 + 12a^{2} > 0 - имеет\ два\ корня.\]

\[x_{1} + x_{2} = - 2;\ \ \ x_{1} \cdot x_{2} = - 3a^{2}\]

\[Искомое\ уравнение\ имеет\ вид:\]

\[y_{1} + y_{2} = \left( x_{1} - 1 \right) + \left( x_{2} - 1 \right) =\]

\[= \left( x_{1} + x_{2} \right) - 2 = - 2 - 2 = - 4.\]

\[y_{1} \cdot y_{2} = \left( x_{1} - 1 \right)\left( x_{2} - 1 \right) =\]

\[= x_{1}x_{2} - \left( x_{1} + x_{2} \right) + 1 =\]

\[= - 3a^{2} - ( - 2) + 1 =\]

\[= - 3a^{2} + 3\]

\[По\ теореме\ Виета:\]

\[p = - \left( y_{1} + y_{2} \right) = - ( - 4) = 4;\]

\[q = y_{1} \cdot y_{2} = - 3a^{2} + 3.\]

\[Искомое\ уравнение\ имеет\ вид:\]

\[y^{2} + 4y - 3a^{2} + 3 = 0.\]