Решите неравенство: |x|*|x-3|+x-2<0.

\[|x| \cdot |x - 3| + x - 2 < 0\]

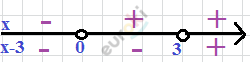
\[1)\ \left\{ \begin{matrix}
x < 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\
- x(3 - x) + x - 2 < 0 \\
\end{matrix} \right.\ \text{\ \ \ \ }\]

\[\left\{ \begin{matrix}
x < 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\
x^{2} - 3x + x - 2 < 0 \\
\end{matrix} \right.\ \text{\ \ \ }\]

\[\left\{ \begin{matrix}
x < 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\
x² - 2x - 2 < 0 \\
\end{matrix} \right.\ \]

\[x^{2} - 2x - 2 = 0\]

\[D = 4 + 8 = 12\]

\[x_{1,2} = \frac{2 \pm 2\sqrt{3}}{2} = 1 \pm \sqrt{3}\]

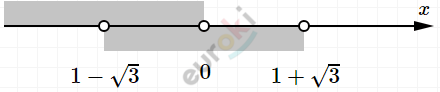
\[\left( 1 - \sqrt{3};0 \right).\]

\[2)\ \left\{ \begin{matrix}
0 \leq x \leq 3\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\
x(3 - x) + x - 2 < 0 \\
\end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix}
0 \leq x \leq 3\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\
- x^{2} + 4x - 2 < 0 \\
\end{matrix} \right.\ \]

\[- x^{2} + 4x - 2 = 0\]

\[D = 16 - 8 = 8\]

\[x_{1,2} = \frac{- 4 \pm 2\sqrt{2}}{- 2} = 2 \pm \sqrt{2}\]

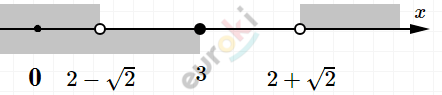
\[\left\lbrack 0;2 - \sqrt{2} \right).\]

\[3)\ \left\{ \begin{matrix}
x > 3\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\
x(x - 3) + x - 2 < 0 \\
\end{matrix} \right.\ \text{\ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix}
x > 3\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\
x^{2} - 3x + x - 2 < 0 \\
\end{matrix} \right.\ \text{\ \ \ \ }\]

\[\left\{ \begin{matrix}
x > 3\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\
x^{2} - 2x - 2 < 0 \\
\end{matrix} \right.\ \text{\ \ \ \ }(см.\ 1)\]

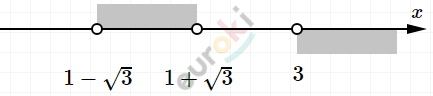
\[\varnothing.\]

\[Ответ:\left( 1 - \sqrt{3};2 - \sqrt{2} \right).\]