При каких значениях m система уравнений x^2+y^2=9; x-y=m: имеет два решения.

\[\left\{ \begin{matrix} x^{2} + y^{2} = 9 \\ x - y = m\ \ \ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ }\left\{ \begin{matrix} x^{2} + y^{2} = 9 \\ y = x - m\ \ \ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ }\]

\[Изобразим\ треугольник\ AOC:\]

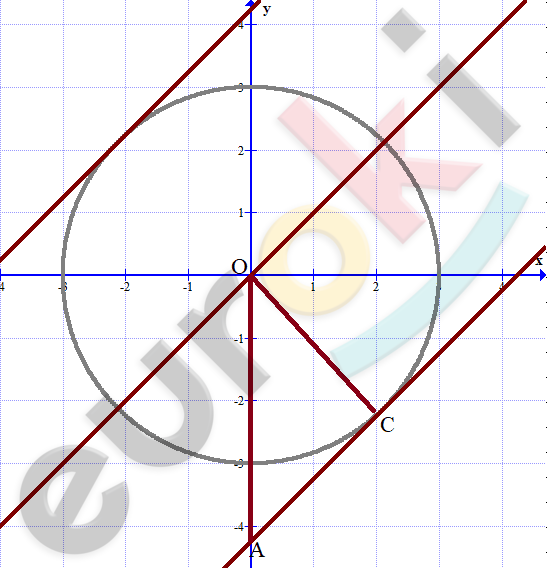
\[\angle C = 90{^\circ};\ \]

\[\angle A = \angle O = 45{^\circ};\]

\[OC = AC = 3\ (радиус);\ \]

\[AO = \sqrt{3^{2} + 3^{2}} = \sqrt{18} = 3\sqrt{2}.\]

\[При\ m \in \left( - 3\sqrt{2};3\sqrt{2} \right):\]

\[две\ точки\ пересечения.\]