При каких значениях m имеет единственный корень уравнение: (m-2)x^2-(2m-4)x+12=0?

\[Уравнение\ имеет\ \]

\[единственный\ корень\ \]

\[при\ D = 0.\]

\[(m - 2)x² - (2m - 4)x + 12 = 0\]

\[m - 2 = 0 \Longrightarrow m = 2.\]

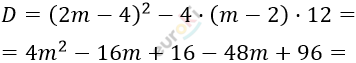
\[= 4m^{2} - 64m + 112 =\]

\[= 4 \cdot \left( m^{2} - 16m + 28 \right)\]

\[4 \cdot \left( m^{2} - 16m + 28 \right) = 0\]

\[m^{2} - 16m + 28 = 0\]

\[D = ( - 16)^{2} - 4 \cdot 1 \cdot 28 =\]

\[= 256 - 112 = 144\]

\[m_{1} = \frac{16 + \sqrt{144}}{2} = \frac{16 + 12}{2} =\]

\[= \frac{28}{2} = 14\]

\[m_{2} = \frac{16 - \sqrt{144}}{2} = \frac{16 - 12}{2} =\]

\[= \frac{4}{2} = 2\]

\[Ответ:при\ m = 14;m = 2.\]