При каких значениях a корни уравнения x^2-(3a+2)x+8a-4a^2=0 больше числа -7?

Ответ:

\[x^{2} - (3a + 2)x + 8a - 4a^{2} = 0\]

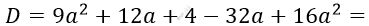
\[= 25a^{2} - 20a + 4 =\]

\[= (5a - 2)^{2} > 0;\ \ \ \ \ \ \ a \neq \frac{2}{5} \neq 0,4\]

\[x_{1} = \frac{3a + 2 - 5a + 2}{2} =\]

\[= \frac{- 2a + 4}{2} = - a + 2\]

\[x_{2} = \frac{3a + 2 + 5a - 2}{2} = \frac{8a}{2} = 4a\]

\[\left\{ \begin{matrix} - a + 2 > - 7 \\ 4a > - 7\ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} a < 9\ \ \ \ \ \ \\ a > - 1\frac{3}{4} \\ \end{matrix} \right.\ \]

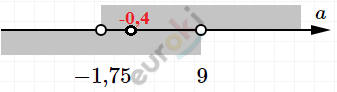
\[Ответ:( - 1,75;0,4) \cup (0,4;9)\text{.\ }\]