Постройте график функции y=x^2-8x+13. Опишите его свойства.

Ответ:

\[y = x^{2} - 8x + 13 =\]

\[= x^{2} - 8x + 16 - 3 =\]

\[= (x - 4)^{2} - 3;\]

\[a = 1 > 0;ветви\ вверх;\]

\[x_{0} = - \frac{b}{2a} = \frac{8}{2} = 4;\]

\[y_{0} = 16 - 32 + 13 = - 3;\]

\[(4; - 3) - вершина.\]

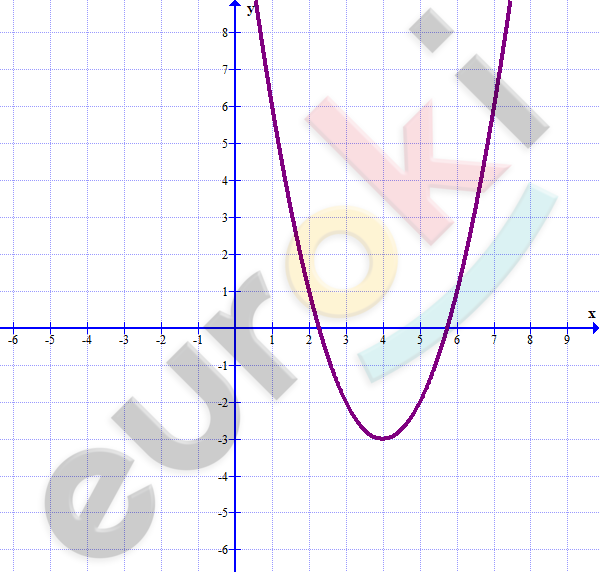
\[D(y) = R;\]

\[E(y) = \lbrack - 3; + \infty).\]

\[Нули\ функции:\]

\[x_{1} \approx 2,2;x_{2} \approx 5,8.\]

\[y > 0\ при\ x < 2,2;x > 5,8;\]

\[y < 0\ при\ 2,2 < x < 5,8.\]

\[Функция\ возрастает\ при\ x > 4;\]

\[функция\ убывает\ при\ x < 4.\]