Постройте график функции y=x^2-2x-8. Найдите с помощью графика: промежуток, в котором функция возрастает.

Ответ:

\[\ f\ возрастает\ при\ x > - 2.\]

\[y = 7x^{2} - 4x\]

\[y = 7 \cdot \left( x - \frac{2}{7} \right)^{2} - \frac{4}{7}\]

\[y_{наим} = y\left( \frac{2}{7} \right) = - \frac{4}{7}.\]

\[y = 2x^{2} - 11x + 5\ \ \ \ \ и\ \ \ y = - 7\]

\[- 7 = 2x^{2} - 11x + 5\]

\[2x^{2} - 11x + 12 = 0\]

\[D = b^{2} - 4ac = 121 - 4 \cdot 2 \cdot 12 =\]

\[= 121 - 96 = 25\]

\[x_{1} = \frac{11 - 5}{4} = \frac{6}{4} = 1,5\]

\[x_{2} = \frac{11 + 5}{4} = \frac{16}{4} = 4\]

\[Ответ:x = 1,5\ \ \ и\ \ \ x = 4.\]

\[y = - x^{2} + 6x - 4\]

\[1)\ x_{0} = \frac{- b}{2a} = \frac{- 6}{- 2} = 3\]

\[y_{0}(3) = - 9 + 18 - 4 = 5.\]

\[2) - x^{2} + 6x - 4 = 0\]

\[x² - 6x + 4 = 0\]

\[D = b^{2} - 4ac = 36 - 4 \cdot 1 \cdot 4 =\]

\[= 36 - 16 = 20\]

\[x_{1} = \frac{6 + 2\sqrt{5}}{2} = 3 + \sqrt{5}\]

\[x_{2} = \frac{6 - 2\sqrt{5}}{2} = 3 - \sqrt{5}\]

\[3)\ x = 0 \Longrightarrow y = - 4\]

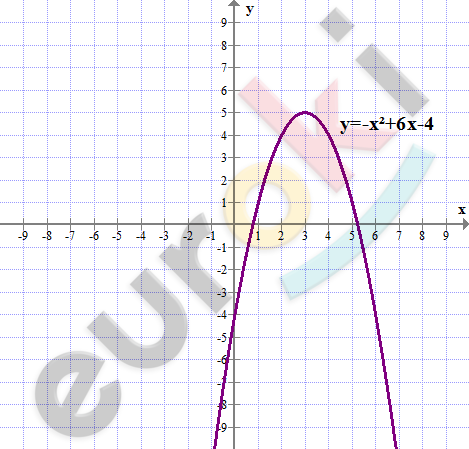
\[\ x = 4,5 \Longrightarrow y = 2,75.\]