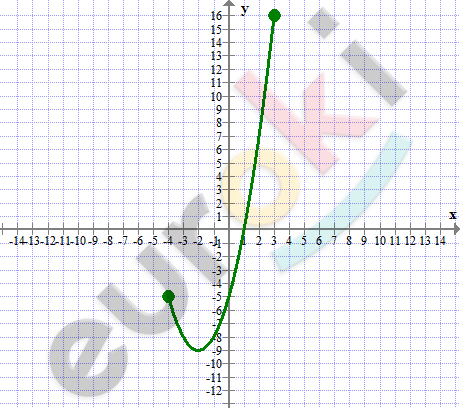
Постройте график функции y=x^2+4x-5, определенной на промежутке [-4; 3]. Пользуясь построенным графиком, найдите область значений данной функции.

Question

Accepted Answer

\[y = x^{2} + 4x - 5,\ \ x \in \lbrack - 4;3\rbrack\]

\[ветви\ вверх\ ,\ \ \]

\[x_{0} = \frac{- 4}{2} = - 2\]

\[y_{0} = 4 - 8 - 5 = - 9\]

\[( - 2;\ - 9)\]

\[x\]	\[- 4\]	\[3\]	\[0\]	\[- 1\]
\[y\]	\[- 5\]	\[16\]	\[- 5\]	\[- 8\]

\[E(y) = \lbrack - 9;16\rbrack\text{\ \ }\]

Ответ: