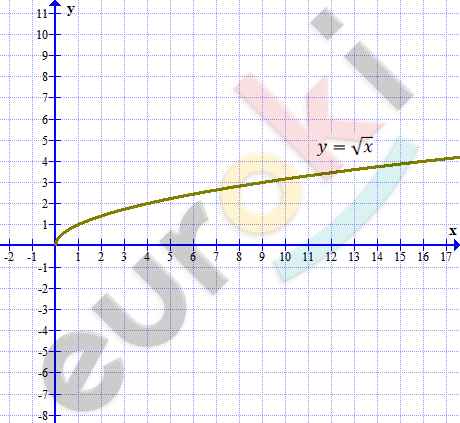
Постройте график функции y=корень из x. Найдите координаты точки пересечения графика этой функции с прямой x-3y+2=0.

Question

Вопрос:

Ответ:

Accepted Answer

\[y = \sqrt{x}\]

\[x\]	\[9\]	\[4\]	\[1\]	\[0\]
\[y\]	\[3\]	\[2\]	\[1\]	\[0\]

\[\left\{ \begin{matrix} x - 3y + 2 = 0 \\ y = \sqrt{x}\text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} 3y = x + 2 \\ y = \sqrt{x}\text{\ \ \ \ \ \ \ } \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} y = \frac{x + 2}{3} \\ y = \sqrt{x}\text{\ \ \ \ \ } \\ \end{matrix} \right.\ \]

\[\frac{x + 2}{3} = \sqrt{x}\ \ \ \ \ \ \ | \cdot 3\]

\[(x + 2)^{2} = \left( 3\sqrt{x} \right)^{2}\]

\[x^{2} + 4x + 4 = 9x\]

\[x^{2} - 5x + 4 = 0\]

\[D = 25 - 16 = 9\]

\[x_{1,2} = \frac{5 \pm 3}{2} = 4;\ \ 1.\]

\[x_{1} = 4;\ \ \ \ \ \ \ \ \ \ \ \ x_{2} = 1\]

\[y_{1}(4) = \sqrt{4} = 2;\ \ \ \ \]

\[y_{2}(1) = \sqrt{1} = 1\]

\[Ответ:(4;2);\ \ (1;1).\]