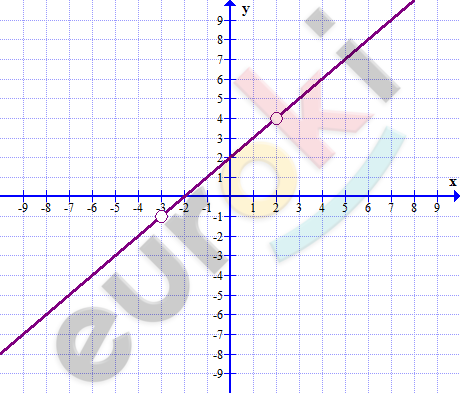
Постройте график функции: y=(2x^2-5x+2)/(x-2)-(x^2-9)/(x+3).

Ответ:

\[y = \frac{2x^{2} - 5x + 2}{x - 2} - \frac{x^{2} - 9}{x + 3} =\]

\[= 2x - 1 - x + 3 = x + 2;\ \ \ \ \]

\[x \neq 2;\ \ \ x \neq - 3\]

\[2x^{2} - 5x + 2 = 0\]

\[x_{1} + x_{2} = 2,5;\ \ \ \ \ \]

\[x_{1} \cdot x_{2} = 1 \Longrightarrow x_{1} = 2;\ \ x_{2} = \frac{1}{2}.\]

\[2x^{2} - 5x + 2 =\]

\[= 2 \cdot (x - 2)\left( x - \frac{1}{2} \right) =\]

\[= (x - 2)(2x - 1)\]

\[y = x + 2\]