Вопрос:
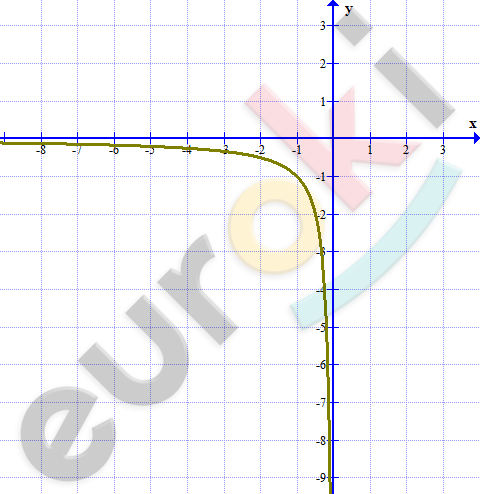
Постройте график функции y=1/x на промежутке (-∞; 0): С помощью определения докажите свое утверждение в пункте «а».
Ответ:
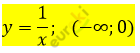
| \[x\] | \[- 1\] | \[- 2\] | \[- 3\] | \[- \frac{1}{2}\] | \[- \frac{1}{3}\] |
|---|---|---|---|---|---|
| \[y\] | \[- 1\] | \[- \frac{1}{2}\] | \[- \frac{1}{3}\] | \[- 2\] | \[- 3\] |
\[x_{1} < x_{2} < 0;\]
\[y_{1} - y_{2} = \frac{1}{x_{1}} - \frac{1}{x_{2}} = \frac{x_{2} - x_{1}}{x_{1}x_{2}} > 0.\]
\[Т.к.\ \ x_{1} < 0,\ \ \ x_{2} < 0,\ \ \ то\ \ \]
\[x_{1} < x_{2}.\]
\[Т.к.\ y_{1} - y_{2} > 0,\ \ \ то\ \]
\[\ y_{1} > y_{2},\ т.е.\ большему\]
\[значению\ аргумента\ \]
\[соответствует\ меньшее\]
\[значение\ функции\ \Longrightarrow\]
\[\Longrightarrow y = \frac{1}{x}\ \ убывает\ на\ ( - \infty;0).\]