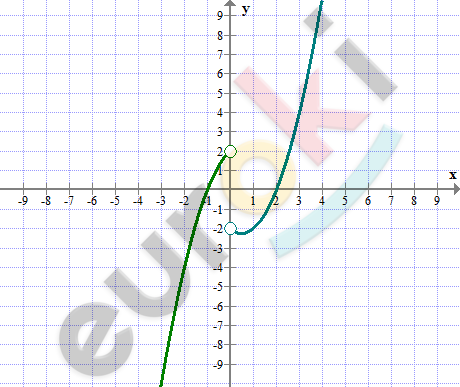
Вопрос:
Постройте график функции: y=|x|/x(x^2-x-2).
Ответ:
\[y = \frac{|x|}{x} \cdot (x^{2} - x - 2)\]
\[y = \left\{ \begin{matrix} x² - x - 2\ \ \ \ \ \ \\ - x^{2} + x + 2\ \ \\ \end{matrix} \right.\ \]
\[x > 0:\]
\[y = x^{2} - x - 2;\ \ a > 0;\ \ \]
\[ветви\ вверх.\]
\[x_{0} = \frac{1}{2};\ \ \ \ \ \ y_{0} = - 2\frac{1}{4};\]
\[\text{\ y}(0) = - 2.\]
\[x < 0:\]
\[y = - x^{2} + x + 2;\ \ a < 0;\ \ \]
\[ветви\ вниз.\]
\[x_{0} = \frac{1}{2};\ \ \ \ \ \ \ y_{0} = 2\frac{1}{4};\ \]
\[y(0) = 2.\]