Площадь прямоугольника 270 см^2. Если одну его сторону увеличить на 6 см, а другую уменьшить на 1,5 см, то получится равновеликий ему прямоугольник. Найдите стороны первого прямоугольника.

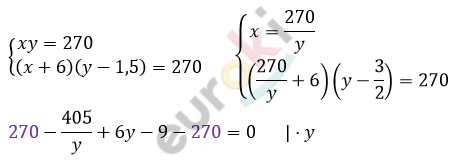
\[- 405 + 6y^{2} - 9y = 0\ \ \ \ \ \ \ |\ :3\]

\[2y^{2} - 3y - 135 = 0\]

\[D = ( - 3)^{2} - 4 \cdot 2 \cdot ( - 135) =\]

\[= 9 + 1080 = 1089;\ \ \ \ \sqrt{D} = 33.\]

\[y_{1} = \frac{3 + 33}{2 \cdot 2} = \frac{36}{4} = 9;\ \ \ \]

\[\text{\ \ }y_{2} = \frac{3 - 33}{2 \cdot 2} = \frac{- 30}{4} =\]

\[= - 7\frac{1}{2}\ \ \ (не\ подходит).\]

\[x = \frac{270}{9} = 30.\]

\[Ответ:9\ см\ и\ 30\ см.\]