Не выполняя построения, найдите координаты точек пересечения: прямой x+2y+2=0 и окружности (x-1)^2+(y-2)^2=5.

Ответ:

\[\left\{ \begin{matrix} x + 2y - 5 = 0,\ \ x = 5 - 2y\ \\ (x - 1)^{2} + (y - 2)^{2} = 5\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

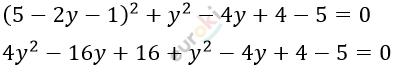
\[5y^{2} - 20y + 15 = 0\ \ \ \ \ \ \ |\ :5\]

\[y^{2} - 4y + 3 = 0\]

\[y_{1} + y_{2} = 4\ \ \ \ \ y_{1} = 1\]

\[y_{1}y_{2} = 3\ \ \ \ \ \ \ \ \ \ y_{2} = 3\]

\[\left\{ \begin{matrix} \ x = 3 \\ y = 1 \\ \end{matrix}\text{\ \ \ \ \ \ \ \ \ } \right.\ \text{\ \ \ \ \ }\left\{ \begin{matrix} x = - 1 \\ y = 3\ \ \ \\ \end{matrix} \right.\ \]

\[Ответ:(3;1),\ ( - 1;3).\]