Найдите значение выражения: (4x+4y)^2/(4x^2-4y^2 ), если x=0,2,y=-0,6.

\[\frac{(4x + 4y)^{2}}{4x^{2} - 4y^{2}};\ если\ \ x = 0,2;\ \ \]

\[y = - 0,6.\]

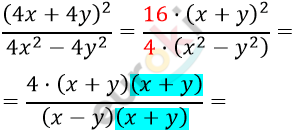
\[= \frac{4 \cdot (x + y)}{x - y} =\]

\[= \frac{4 \cdot \left( 0,2 + ( - 0,6) \right)}{0,2 - ( - 0,6)} =\]

\[= \frac{4 \cdot (0,2 - 0,6)}{0,2 + 0,6} = \frac{4 \cdot ( - 0,4)}{0,8} =\]

\[= - \frac{4 \cdot 0,4}{0,8} = - 2.\]