Найдите все значения параметра a, для каждого из которых множество решений неравенства x^2-(7a+5)x+12a^2+20a<0 содержит отрезок [5; 8].

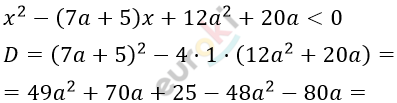
\[= a^{2} - 10a + 25 = (a - 5)^{2}.\]

\[При\ a = 5:единственный\ \]

\[корень,\ неравенство\ можно\ \]

\[записать\ в\ виде:\]

\[(x - 20)^{2} < 0 \Longrightarrow нет\ решения.\]

\[При\ a > 5:\ \ x_{1} = 4a;\ \ \ \]

\[x_{2} = 3a + 5;\ \ x_{1} > x_{2}\ \]

\[\Longrightarrow решение\ \left( x_{2};x_{1} \right)\ \]

\[не\ содержит\ отрезок\ \lbrack 5;8\rbrack;\ \ \]

\[так\ как\text{\ \ x}_{1} > x_{2} > 20.\ \]

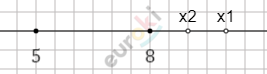
\[При\ a < 5:\ \ x_{1} = 4a;\ \ \ \]

\[x_{2} = 3a + 5;\ x_{2} > x_{1}\]

\[\Longrightarrow решение\ \left( x_{1};x_{2} \right)\ содержит\ \]

\[отрезок\ \lbrack 5;8\rbrack,\ если\ x_{1} < 5\ \]

\[и\ \ x_{2} > 8 \Longrightarrow\]

\[4a < 5\ \ \ и\ \ \ 3a + 5 > 8 \Longrightarrow\]

\[\Longrightarrow a < 1\frac{1}{4}\ и\ \ 3a > 3 \Longrightarrow\]

\[\Longrightarrow a < 1\frac{1}{4}\ и\ \ a > 1 \Longrightarrow\]

\[\Longrightarrow a \in \left( 1;1\frac{1}{4} \right)\text{.\ }\]

\[Ответ:\ a \in \left( 1;1\frac{1}{4} \right)\text{.\ }\]