Найдите целые решения системы неравенств 4*(5x-4)>=13*(x-1)+18; x(x+5)-(x-2)(x+8)>9.

Ответ:

\[\left\{ \begin{matrix} 4 \cdot (5x - 4) \geq 13 \cdot (x - 1) + 18 \\ x(x + 5) - (x - 2)(x + 8) > 9\ \ \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} 20x - 16 \geq 13x - 13 + 18\ \ \ \ \ \ \ \ \ \ \ \ \\ x^{2} + 5x - x^{2} - 8x + 2x + 16 > 9 \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} 7x \geq 21\ \\ - x > - 7 \\ \end{matrix} \right.\ \Longrightarrow \left\{ \begin{matrix} x \geq 3 \\ x < 7 \\ \end{matrix} \right.\ \]

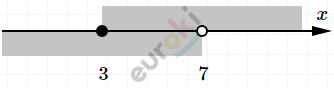
\[Целые\ решения:3;4;5;6.\]

\[Ответ:\ 3;4;5;6.\]