Найдите сумму двадцати первых членов арифметической прогрессии (an), если a7+a13=21 и a8+a12-a15=3.

Ответ:

\[\left\{ \begin{matrix} a_{7} + a_{13} = 21\ \ \ \ \ \ \ \ \ \\ a_{8} + a_{12} - a_{15} = 3 \\ \end{matrix}\text{\ \ \ \ \ \ \ \ } \right.\ \]

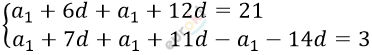
\[\left\{ \begin{matrix} 2a_{1} + 18d - 21 = 0\ \ \ \ \ \\ a_{1} + 4d - 3 = 0\ \ \ \ \ \ | \cdot 2 \\ \end{matrix}\text{\ \ \ \ \ } \right.\ \]

\[\left\{ \begin{matrix} 2a_{1} + 18d - 21 = 0 \\ 2a_{1} + 8d - 6 = 0\ \ \ \ \\ \end{matrix}\ \ ( - )\ \ \ \right.\ \]

\[\left\{ \begin{matrix} 10d = 15\ \ \ \ \ \ \ \ \ \ \ \\ a_{1} = \frac{6 - 8d}{2}\text{\ \ \ \ \ \ } \\ \end{matrix}\text{\ \ \ \ \ \ \ \ \ \ \ \ \ }\left\{ \begin{matrix} d = 1,5\ \\ a_{1} = - 3 \\ \end{matrix} \right.\ \right.\ \]

\[S_{20} = \frac{2a_{1} + 19d}{2} \cdot 20 =\]

\[= \left( {2a}_{1} + 19d \right) \cdot 10 =\]

\[= ( - 6 + 28,5) \cdot 10 =\]

\[= 10 \cdot 22,5 = 225.\]

\[Ответ:225.\ \]