Найдите решение неравенства 3/(x+1)≤5/(x+2).

\[\frac{3}{x + 1} \leq \frac{5}{x + 2}\]

\[\frac{3^{\backslash x + 2}}{x + 1} - \frac{5^{\backslash x + 1}}{x + 2} \leq 0\]

\[\frac{3x + 6 - 5x - 5}{(x + 1)(x + 2)} \leq 0\]

\[\frac{- 2x + 1}{(x + 1)(x + 2)} \leq 0\]

\[- 2x = - 1\]

\[x = \frac{1}{2} = 0,5.\]

\[x \neq - 1;\ \ x \neq - 2.\]

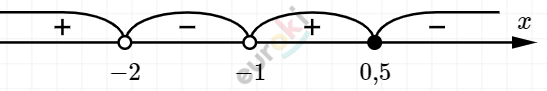
\[Ответ:x \in ( - 2; - 1) \cup \lbrack 0,5; + \infty).\]