Найдите первый член и знаменатель геометрической прогрессии (bn), если: b2+b5=56 и b3-b4+b5=14.

Ответ:

\[b_{2} + b_{5} = 56;\ \ \]

\[b_{3} - b_{4} + b_{5} = 14:\]

\[\left\{ \begin{matrix} b_{1}q + b_{1}q^{4} = 56\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ b_{1}q^{2} - b_{1}q^{3} + b_{1}q^{4} = 14 \\ \end{matrix}\text{\ \ \ \ \ \ \ } \right.\ \]

\[\left\{ \begin{matrix} b_{1}q\left( 1 + q^{3} \right) = 56\ \ \ \ \ \ \ \ \ \ \ \\ b_{1}q\left( q - q^{2} + q^{3} \right) = 14 \\ \end{matrix}\text{\ \ \ \ \ \ \ \ \ } \right.\ \]

\[\ \frac{1 + q^{3}}{q - q^{2} + q^{3}} = 4\]

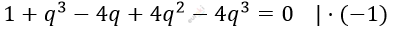
\[3q^{3} - 4q^{2} + 4q - 1 = 0\]

\[\left( q - \frac{1}{3} \right)\left( 3q^{2} - 3q + 3 \right) = 0\]

\[q = \frac{1}{3}\ \ или\ \ \ \ \ q^{2} - q + 1 = 0\]

\[\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ D = 1 - 4 < 0\]

\[q = \frac{1}{3}:\]

\[b_{1} = \frac{56}{q\left( 1 + q^{3} \right)} = \frac{56}{\frac{1}{3} \cdot \left( 1 + \frac{1}{27} \right)} =\]

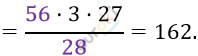
\[Ответ:q = \frac{1}{3};\ \ \ b_{1} = 162.\]