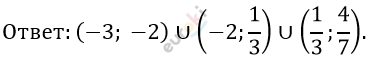Вопрос:
Найдите область определения функции: y=(x+14)/корень из (12-17x-7x^2 )-(x-14)/(3x^2+5x-2).
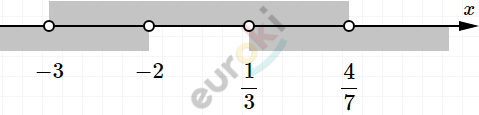
Ответ:
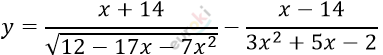
\[\left\{ \begin{matrix}
12 - 17x - 7x^{2} > 0 \\
3x² + 5x - 2
eq 0\ \ \ \ \\
\end{matrix} \right.\ \]
\[12 - 17x - 7x^{2} = 0\]
\[D = 289 + 336 = 625\]
\[x_{1} = \frac{17 + 25}{- 14} = - 3\]
\[x_{2} = \frac{17 - 25}{- 14} = \frac{4}{7}\]
\[3x^{2} + 5x - 2 = 0\]
\[D = 25 + 24 = 49\]
\[x_{1}
eq \frac{- 5 + 7}{6} = \frac{1}{3}\]
\[x_{2}
eq \frac{- 5 - 7}{6} = - 2\]