Найдите область определения функции: f(x)=корень из (x-6)/корень из (x+3)+(5x-4)/(x^2-8x+7).

\[f(x) = \frac{\sqrt{x - 6\ }}{\sqrt{x + 3}} + \frac{5x - 4}{x^{2} - 8x + 7}\]

\[\left\{ \begin{matrix} x - 6 \geq 0\ \ \ \ \ \ \ \ \ \ \ \ \\ x + 3 > 0\ \ \ \ \ \ \ \ \ \ \ \ \\ x^{2} - 8x + 7
eq 0 \\ \end{matrix}\text{\ \ \ \ \ \ \ } \right.\ \]

\[\left\{ \begin{matrix} x \geq 6\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ x > - 3\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ (x - 1)(x - 7)
eq 0 \\ \end{matrix}\text{\ \ \ \ \ \ \ } \right.\ \]

\[\left\{ \begin{matrix} x \geq 6 \\ x
eq 1 \\ x
eq 7 \\ \end{matrix} \right.\ \ \]

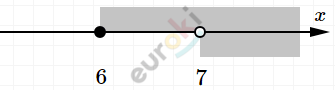
\[\Longrightarrow \lbrack 6;\ \ 7) \cup (7;\ + \infty).\]