Вопрос:
Найдите множество решений неравенства: (x^2-4x)/8+(x-3)/5>=(1-x)/6.
Ответ:
\[\frac{x^{2} - 4x}{8} + \frac{x - 3}{5} \geq \frac{1 - x}{6}\ \ \ | \cdot 120\]
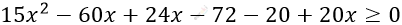
\[15x^{2} - 16x - 92 \geq 0\]
\[D = 256 + 5520 = 5776 = 76^{2}\]
\[x_{1} = \frac{16 + 76}{30} = 3\frac{1}{15}\]
\[x_{2} = \frac{16 - 76}{30} = - 2\]
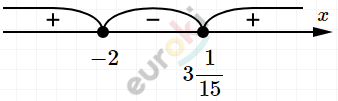
\[Ответ:( - \infty;\ - 2\rbrack\left\lbrack 3\frac{1}{15}; + \infty \right).\]