Найдите множество решений неравенства: (x+3)^2-16>=(1-2x)^2.

Ответ:

\[(x + 3)^{2} - 16 \geq (1 - 2x)^{2}\]

\[x^{2} + 6x + 9 - 16 \geq 1 - 4x + 4x^{2}\]

\[- 3x^{2} + 10x - 8 \geq 0\]

\[- 3x^{2} + 10x - 8 = 0\]

\[D = 100 - 96 = 4\]

\[x_{1} = \frac{- 10 + 2}{- 6} = 1\frac{1}{3}\]

\[x_{2} = \frac{- 10 - 2}{- 6} = 2\]

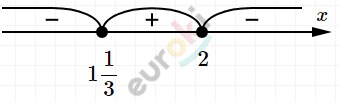
\[Ответ:\ \ x \in \left\lbrack 1\frac{1}{3};\ \ 2 \right\rbrack.\]