Найдите корни уравнения: x/(x+2)+(x+1)/(x+5)-(7-x)/(x^2+7x+10)=0.

Ответ:

\[\frac{x}{x + 2} + \frac{x + 1}{x + 5} - \frac{7 - x}{x^{2} + 7x + 10} =\]

\[= 0\]

\[x^{2} + 7x + 10 = (x + 5)(x + 2)\]

\[x_{1} + x_{2} = - 7;\ \ \ x_{1} \cdot x_{2} = 10\]

\[x_{1} = - 2;\ \ x_{2} = - 5.\]

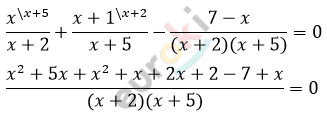
\[\frac{2x^{2} + 9x - 5}{(x + 2)(x + 5)} = 0\]

\[2x^{2} + 9x - 5 =\]

\[= 2 \cdot (x - 0,5)(x + 5) =\]

\[= (2x - 1)(x + 5)\]

\[D = 81 + 40 = 121\]

\[x_{1} = \frac{- 9 + 11}{4} = 0,5;\ \ \ \]

\[\ x_{2} = \frac{- 9 - 11}{4} = - 5.\]

\[\frac{(2x - 1)(x + 5)}{(x + 2)(x + 5)} = 0;\ \ \ \ \]

\[\ x \neq - 2;\ \ x \neq - 5\]

\[2x - 1 = 0\]

\[x = \frac{1}{2}\]

\[x = 0,5.\]

\[Ответ:x = 0,5.\]