Найдите корни уравнения: (4x^2+x)/3-(5x-1)/6=(x^2+17)/9.

Ответ:

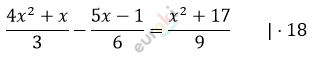
\[6 \cdot \left( 4x^{2} + x \right) - 3 \cdot (5x - 1) =\]

\[= 2 \cdot \left( x^{2} + 17 \right)\]

\[24x^{2} + 6x - 15x + 3 =\]

\[= 2x^{2} + 34\]

\[24x^{2} - 9x + 3 - 2x^{2} - 34 = 0\]

\[22x² - 9x - 31 = 0\ \]

\[D = b^{2} - 4ac =\]

\[= 81 - 4 \cdot 22 \cdot ( - 31) =\]

\[= 81 + 2728 = 2809\]

\[x_{1} = \frac{9 + 53}{44} = \frac{62}{44} = \frac{31}{22} = 1\frac{9}{22}\]

\[x_{2} = \frac{9 - 53}{44} = - \frac{44}{44} = - 1\]

\[Ответ:x_{1} = 1\frac{9}{22};\ \ x_{2} = - 1.\]