Найдите четыре последовательных натуральных числа таких, что произведение четвёртого и второго из этих чисел на 13 больше произведения третьего и первого.

\[Пусть\ n,\ n + 1,\ n + 2,\ n + 3 -\]

\[четыре\ последовательных\ \]

\[натуральных\ числа,\ тогда:\]

\[(n + 3)(n + 1) - (n + 2)n = 13\]

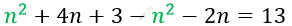
\[2n = 10\]

\[n = 5 - первое\ число.\]

\[n + 1 = 5 + 1 = 6 - второе\ \]

\[число.\]

\[n + 2 = 5 + 2 = 7 - третье\ \]

\[число.\]

\[n + 3 = 5 + 3 = 8 - четвертое\ \]

\[число.\]

\[Ответ:5,\ 6,\ 7,\ 8.\ \]