Моторная лодка прошла по течению реки 16 км, а против течения 6 км, затратив на весь путь 1 ч 30 мин. Найдите собственную скорость моторной лодки, если скорость течения равна 2 км/ч.

\[Пусть\ x\ \frac{км}{ч} - собственная\ \]

\[скорость\ моторной\ лодки.\]

\[(x + 2)\ \frac{км}{ч} - скорость\ \]

\[лодки\ по\ течению\ реки;\]

\[(x - 2)\ \frac{км}{ч} - скорость\ \]

\[против\ течения.\]

\[На\ весь\ путь\ потрачено\ \]

\[1\ ч\ 30\ мин = 1\frac{1}{2}\ ч = \frac{3}{2}\ ч.\]

\[Составим\ уравнение:\]

\[\frac{16^{\backslash x - 2}}{x + 2} + \frac{6^{\backslash x + 2}}{x - 2} = \frac{3^{\backslash(x - 2)(x + 2)}}{2}\]

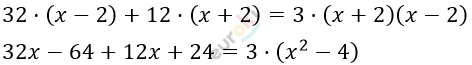
\[44x - 40 = 3x^{2} - 12\]

\[3x^{2} - 44x - 12 + 40 = 0\]

\[3x^{2} - 44x + 28 = 0\]

\[x_{1} = \frac{2}{3}\ (не\ подходит);\ \ \ \]

\[x_{2} = 14\ \left( \frac{км}{ч} \right) - собственная\ \]

\[скорость\ моторной\ лодки.\]

\[Ответ:14\ \frac{км}{ч}.\]